Bonjour,
De vous laisser y réfléchir un minimum je suppose, les éléments nécessaires étant déjà là ...
Supposons que 1(x) admette une limite l en

.
En appliquant la définition de la limite pour
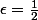
, on trouve qu'il existe A réel tel que pour tout réel
 - l| < \frac{1}{2})
.
Or on peut trouver x supérieur à A tel que 1(x) = 0 et x supérieur à A tel que 1(x) = 1, donc on en déduit notamment que
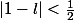
et que
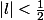
.
De |1 - l| < 1/2 on en déduit 1 - l < 1/2 donc 1/2 < l, et de |l| < 1/2 on en déduit l < 1/2.
C'est absurde, donc la fonction ne peut admettre une limite finie (ni infinie ...) en plus l'infini.
Le raisonnement utilisé est certes légèrement différent de celui de LB2, mais les idées sont les mêmes. Pour reprendre les points de sa démonstration (de manière non formelle):
- l = 0 ou l = 1, car sinon en prenant epsilon suffisamment petit, on aurait, à partir d'un certain rang, |1(x) - l| < epsilon et notamment 1(x) différent de 0 et de 1, ce qui est absurde.
-En reprenant la définition de la limite pour epsilon = 1/2 par exemple, on aurait, toujours à partir d'un certain rang, |1(x) - l| < 1/2, donc nécessairement 1(x) = l (car si l = 0, 1(x) ne peut être égal à 1, de même dans l'autre sens).

