Nombre d'or et rectangle d'or

[cecy3]

Voici une construction du rectangle d'or.
ABCD est un carré de côté de longueur a.

L'arc de cercle de centre I milieu de [AB], passe par les points D , C et E
1.Déterminer en fonction de a les dimensiosn des rectangles BEPC et ADPE.
En déduire que ces 2 rectangles ont le même format dont on donnera la valeur exacte puis l'arrondi d'ordre 3.
Ce nimbre s'appelle p (phi)

2.On appelle b la longueur BE

a) exprimer en focntion de a et de b les quotients AE/AD et PE/BE puis les exprimer en fonction de p (phi).

b) Les rectangles BEPC et ADPE ayant le même format, montrer que p(phi) est une solution de l'équation x²-x-1=0

c) Montrer que x²-x-1=0(x-1/2)²-5/4

d)Factoriser x²-x-1 puis résoudre l'équation x²-x-1=0
Retrouver la valeur p (phi) obtenue a la question 1.

[zebdebda]

euh... comment sont construits les points P et E ?

[cecy3]

D_______________c_________p




A_______________b_________e

[zebdebda]

Ok je pense avoir la figure : je suppose que E est l'intersection de (AB) et du cercle, puis on complète pour que BEPC soit un rectangle.

Il te faut le rayon du cercle pour avoir la longueur BE, et ainsi l'aire de BEPC.

Pour calculer le rayon, travaille dans le triangle AID.

[cecy3]

non la figure est tte faite je n'ai rien a compléter

[cecy3]

le rayon du cercle est [IE]

[cecy3]

je ne vois pas comment on peut trouver le rayon avec le triangle AID

[zebdebda]

[ID] est aussi un rayon du cercle, puisque I est le centre et que le cercle passe par D
Le triangle AID est rectangle en A et tu connais la longueur des côtés de l'angle droit. Tu peux donc calculer l'hypothénuse

[cecy3]

je trouve DI=a^3/2

[zebdebda]

Je trouve
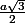
Une faute de frappe peut-être.

Donc IE vaut aussi
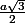
Quelle est donc la longueur de BE ?

[cecy3]

BE=AE-BE
BE=a+BE-av3/2

[cecy3]

je voudrais savoir si c ça