Bonjour j'ai le problème suivant mais je sais pas si mon approche est bonne pour la résolution:
Q1 A l’aide d’une méthode numérique inconnue on a calculé l’intégrale de la fonction
sin(x) entre 0 et π/2 pour différentes valeurs du pas d’intégration h.
On a obtenu les résultats suivants :
h valeur de l’intégrale
_________________________
0.4 1.078 979
0.2 1.009 872
0.1 1.001 235
Compte tenu de la valeur exacte de cette intégrale, pouvez-vous utiliser ces informations
pour en déduire l’ordre probable de cette méthode ? Expliquez votre démarche ou vos
essais de démarches.
(Ce résultat devrait en pratique au moins être corroboré par un test de la méthode sur
d’autres intégrales connues pour être fiable et si possible par une approche théorique –
néanmoins vous pouvez déjà énoncer une hypothèse)
Résolution :
Je pense à procéder de la manière suivante :
Je vais appliquer les 3 méthodes que nous avons vu en classe :
Simpson, Rectangle et Trapèzes à ma fonction sin(x) pour un pas de 0.4
et ensuite comparer mes résultats aux résultats théorique , la méthode qui se rapprocherait le plus des résultats théorique serait donc la méthode numérique inconnue , pour être tout à fait sûr je vais faire la même chose pour le pas de 0.2 et 0.1.
Qu'en pensez-vous?
Calcul numérique intégration
13 messages
- Page 1 sur 1
Re: Calcul numérique intégration
Je pense que tu devrais revoir la définition de l'ordre d'une méthode numérique, et revoir comment varie l'erreur en fonction du pas d'intégration pour une méthode d'ordre  .
.
On connaît bien sûr la valeur exacte de l'intégrale que l'on calcule numériquement.
Quand on divise le pas d'intégration par 2 (passer de 0.4 à 0.2, puis 0.1), par combien est divisée l'erreur, en gros ?
On connaît bien sûr la valeur exacte de l'intégrale que l'on calcule numériquement.
Quand on divise le pas d'intégration par 2 (passer de 0.4 à 0.2, puis 0.1), par combien est divisée l'erreur, en gros ?
Re: Calcul numérique intégration
Tout dépend de la méthode utiliser
Je sais que pour l'approximation par la méthode des rectangle qui est d'ordre 1 , c'est à dire}{n}*h^{1}*C_{1}) à chaque fois qu'on divise le pas par deux l'erreur est diviser également par 2.
à chaque fois qu'on divise le pas par deux l'erreur est diviser également par 2.
Pour la méthode des trapèzes qui est d'ordre 2 , on a comme erreur}{12}C_{2}*h^{2}) Dés lors quand on va diviser le pas par deux , l'erreur sera diviser par 4.
Dés lors quand on va diviser le pas par deux , l'erreur sera diviser par 4.
Pour la méthode de Simpson qui est d'ordre 4 en divisant le pas par 4 on va diviser l'erreur par 16.
c'est exacte ?
Je sais que pour l'approximation par la méthode des rectangle qui est d'ordre 1 , c'est à dire
Pour la méthode des trapèzes qui est d'ordre 2 , on a comme erreur
Pour la méthode de Simpson qui est d'ordre 4 en divisant le pas par 4 on va diviser l'erreur par 16.
c'est exacte ?
Re: Calcul numérique intégration
slt,
ben non, si tu divises le pas par 4, avec simpson dont l'erreur est d'ordre 4, ton erreur sera de l'ordre de (h/4)^4 idem tu divises par 4^4=256
Je pense que l'approche que te suggère gbzm est de regarder les erreurs qui te sont données:
0.4 -> 0.078
0.2 -> 0.009
en remarquant que:
|e| <= C * h^n (pour n un ordre donné), et C une constante liée à ta méthode
on déduit:
e_{0.4} = C0.4^n
e_{0.2} = C0.2^n et tu cherches n (faut réléchir par rapport à la valeur flottante trouvée)
Avec un peu de chance tu trouves un n "plausible". Pour confirmer par l'xp que il est bon:
oui tu peux regarder tes méthodes de "références" et regarder si ca à l'air de matcher avec ta méthode inconnue de même ordre.
mais si tu peux appliquer ta méthode inconnue, pe tu peux tenter de retrouver la constante C et voir si ... elle reste la même pour les pas différents!
Pour la méthode de Simpson qui est d'ordre 4 en divisant le pas par 4 on va diviser l'erreur par 16.
ben non, si tu divises le pas par 4, avec simpson dont l'erreur est d'ordre 4, ton erreur sera de l'ordre de (h/4)^4 idem tu divises par 4^4=256
Je pense que l'approche que te suggère gbzm est de regarder les erreurs qui te sont données:
0.4 -> 0.078
0.2 -> 0.009
en remarquant que:
|e| <= C * h^n (pour n un ordre donné), et C une constante liée à ta méthode
on déduit:
e_{0.4} = C0.4^n
e_{0.2} = C0.2^n et tu cherches n (faut réléchir par rapport à la valeur flottante trouvée)
Avec un peu de chance tu trouves un n "plausible". Pour confirmer par l'xp que il est bon:
oui tu peux regarder tes méthodes de "références" et regarder si ca à l'air de matcher avec ta méthode inconnue de même ordre.
mais si tu peux appliquer ta méthode inconnue, pe tu peux tenter de retrouver la constante C et voir si ... elle reste la même pour les pas différents!
la vie est une fête 
Re: Calcul numérique intégration
Voici :
Avec la première approche :
J'ai deux équation à deux inconnues :
 (1)
(1)
 (2)
(2)
 (3)
(3)
(3) ==>(2) ==>
 + log(0,078) - n*log(4) = log(0,009))
 -log(4^{n}) = log(0,009))
 = log(0,009))
 -log(4^n) = log(0,009))
......
je retrouve un n qui vaut n = 3,11 donc un ordre supérieur à 3 j'ai considérer que c'était la méthode de Simpson et en faisant les calculs avec la méthode de Simpson pour le pas donnée je retrouve sensiblement les même valeurs.
j'en déduis donc que la méthode inconnu est la méthode de simpson
Avec la première approche :
J'ai deux équation à deux inconnues :
(3) ==>(2) ==>
......
je retrouve un n qui vaut n = 3,11 donc un ordre supérieur à 3 j'ai considérer que c'était la méthode de Simpson et en faisant les calculs avec la méthode de Simpson pour le pas donnée je retrouve sensiblement les même valeurs.
j'en déduis donc que la méthode inconnu est la méthode de simpson
Re: Calcul numérique intégration
Pourquoi réponds-tu à une question qu'on ne te pose pas ? On ne te demande pas quelle est la méthode numérique, on te demande l'ordre de la méthode numérique.
Re: Calcul numérique intégration
Mmh...
Moi je vois que quand le pas est divisé par 2, l'erreur est à peu près divisée par 8 : quand le pas passe de 0.4 à 0.2, l'erreur passe de 0.08 à 0.01 ; quand le pas passe de 0.2 à 0.1, l'erreur passe de de 0.01 à 0.00125.
Tu es sûr que ça fait de l'ordre 4 ????
Quand est divisé par 2, par combien est divisé
est divisé par 2, par combien est divisé 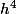 ???
???
Moi je vois que quand le pas est divisé par 2, l'erreur est à peu près divisée par 8 : quand le pas passe de 0.4 à 0.2, l'erreur passe de 0.08 à 0.01 ; quand le pas passe de 0.2 à 0.1, l'erreur passe de de 0.01 à 0.00125.
Tu es sûr que ça fait de l'ordre 4 ????
Quand
Re: Calcul numérique intégration
Quand h est divisé par 2 , h^4 est divisé par 16 , hors c'est pas notre car on une division 2 fois moindres , par élimination je dirai donc que c'est une méthode d'ordre 2. pourtant par calcul je trouve n =3... :s
Re: Calcul numérique intégration
Brut de décoffrage, je répondrais alors que l'ordre de la méthode est 3.
mais si on peut pas avoir un ordre impair (>2), alors tu as le choix entre 2 et 4.
Qui peut le plus peut le moins, tu peux répondre 2 et si ya la borne théorique est plus large que les erreurs obtenues... ben t'as eu de la chance avec ta méthode.
Si tu réponds 4, faut checker que l'erreur obtenue est inférieure à la borne théorique...
(donc remplace et vérifies que le C est possible/stable pour e_0.4, e_0.2, e_0.1)
pour info, j'ai testé trapèze et ca donne à peu pres les même erreurs
mais si on peut pas avoir un ordre impair (>2), alors tu as le choix entre 2 et 4.
Qui peut le plus peut le moins, tu peux répondre 2 et si ya la borne théorique est plus large que les erreurs obtenues... ben t'as eu de la chance avec ta méthode.
Si tu réponds 4, faut checker que l'erreur obtenue est inférieure à la borne théorique...
(donc remplace et vérifies que le C est possible/stable pour e_0.4, e_0.2, e_0.1)
pour info, j'ai testé trapèze et ca donne à peu pres les même erreurs
la vie est une fête 
Re: Calcul numérique intégration
Dans un calcul, tu trouves 3.11 ; bizarre, Je trouve plutôt 3.00005 , ou encore 2.999 ... il doit y avoir un truc faux dans le calcul. Ce serait bien que tu revoies ton calcul.
Et même si on trouve 3.11, il n'est pas question d'arrondir à 4, parce que 4, ça correspondrait à un truc connu.
Et même si on trouve 3.11, il n'est pas question d'arrondir à 4, parce que 4, ça correspondrait à un truc connu.
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
