Convergence uniforme et points critiques

[Lostounet]

Bonsoir,

Soit K un compact de
Soit une suite de fonctions polynomiales convergeant uniformément vers une fonction sur K. P est une fonction de classe C^k(K)

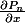
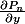
Quels résultats a-t-on sur la convergence des suites des dérivées partielles et ? Peut-on dire que les points critiques des se rapprochent de ceux de ?

[GaBuZoMeu]

Bonjour,

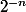
Mmh ... Déjà à une variable, sur [0,1], tu peux avoir une suite de polynômes qui converge uniformément vers la fonction identité et telle que la suite des dérivés fait n'importe quoi : avec Stone -Weierstrass, tu peux approcher par un polynôme la fonction avec sa dérivée aussi près que tu veux, disons à près. 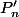Tu vois que la suite tex](P_n)[/tex] converge uniformémement vers la fonction identité sur tandis que les dérivés , proches de , sont catastrophiques.

Alors, qu'espères-tu ? Tu as peut-être quelque chose derrière la tête ?

[Lostounet]

Effectivement c'est un bon exemple ! Merci.

Je souhaitais savoir s'il valait mieux approximer le gradient de la fonction P par des suites polynomiales ou bien s'il valait mieux approximer la fonction P par des Pn en elle-même pour approcher les points critiques...

[GaBuZoMeu]

Approcher la fonction ne donne pas de contrôle sur les dérivées a priori.

[Lostounet]

Approcher la fonction ne donne pas de contrôle sur les dérivées a priori.

Merci bien !