Inégalité
Olympiades mathématiques, énigmes et défis
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 01 Juil 2019, 21:15
par MMu » 01 Juil 2019, 21:15
Soient

rééls positifs
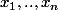
tels que
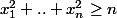
.
Montrer que
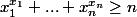

-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 01 Juil 2019, 22:26
par lyceen95 » 01 Juil 2019, 22:26
La propriété est fausse.
Contre exemple :
x1= racine(2)
x2=0.0001
n=2
Je suppose qu'il manque la condition x1 <= x2 <= ... <= xn
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 01 Juil 2019, 22:55
par MMu » 01 Juil 2019, 22:55
lyceen95 a écrit:La propriété est fausse.
Contre exemple :
x1= racine(2)
x2=0.0001
n=2
Je suppose qu'il manque la condition x1 <= x2 <= ... <= xn

très drôle


-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 01 Juil 2019, 22:58
par lyceen95 » 01 Juil 2019, 22:58
Oups.
J'avais vu x1^1 + ... + xn^n au lieu de x1^x1 + ... + xn^xn.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Juil 2019, 23:03
par Ben314 » 07 Juil 2019, 23:03
Salut,
Par du gros calcul brutal :
Pour
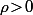
fixé et
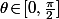
on pose
\!=\!\rho\cos(\theta))
;
\!=\!\rho\sin(\theta))
puis on pose
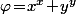
.
La fonction

est continue
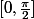
et dérivable sur
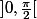
( où
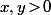
) avec
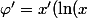\!+\!1)x^x\!+\!y'(\ln(y)\!+\!1)y^y=-y(\ln(x)\!+\!1)x^x\!+\!x(\ln(y)\!+\!1)y^y)
\!+\!1)y^{y-1}\!>\!(\ln(x)\!+\!1)x^{x-1})
.
Or, si pour
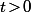
on pose
\!=\!(\ln(t)\!+\!1)t^{t-1})
alors
\!=\!t^{t-2}\!+\! (\ln(t)\!+\!1)(\ln(t)\!+\!1\!-\!\frac{1}{t})t^{t-1})
et on a donc
\!>\!0\ \Leftrightarrow\ (\ln(t)\!+\!1)^2\!>\!\dfrac{\ln(t)}{t})
qui est trivialement vérifié à la fois sur
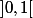
où
\!+\!1)^2\!\geq\!0\!>\!\!\dfrac{\ln(t)}{t})
mais aussi sur
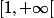
où
\!+\!1)^2\!>\ln(t)\!\geq\!\dfrac{\ln(t)}{t})
.
Donc

est strictement croissante sur

et on a
\!>\!\psi(x)\ \Leftrightarrow\ y\!>\!x)
.
Tout cela montre que, pour une valeur fixée de
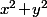
(avec
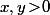
) la valeur minimale de
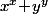
est obtenue lorsque

. Et bien sûr c'est la même chose avec plus de 2 variables vu que si deux d'entre elles étaient différentes, on pourrait faire diminuer la somme des
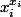
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 08 Juil 2019, 12:56
par MMu » 08 Juil 2019, 12:56
On peut faire un peu plus simple en étudiant
=x^x-\frac{x^2+1}2)
=x^x(1+\ln x)^2+x^{x-1}-1>0)
)
=x^x(1+\ln x)-x)
, croissante avec
=0)
Il s'ensuit que le minimum de

est
=0)
On a donc
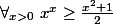
et donc
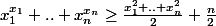

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités

 très drôle
très drôle 
