Je n'arrive pas à effectuer les IPP nécessaires pour montrer le résultat de la question 1.5 et 1.6
Merci d'avance
IPP
4 messages
- Page 1 sur 1
Re: IPP
par aviateur » 23 Juin 2019, 11:37
Bonjour
Pour 1.5, m>n
^m \int_{\R} H_n(x) \dfrac{d^m}{dx^m} e^{-x^2} dx)
une IPP donne
^m [ H_n(x) \dfrac{d^{m-1} }{dx^{m-1}} e^{-x^2} H_n(x)]_{-\infty}^{+\infty} -(-1)^m \int_{\R} H_n'(x) \dfrac{d^{m-1} }{dx^{m-1}} e^{-x^2} dx)
^{m+1} \int_{\R} H_n'(x) \dfrac{d^{m-1} }{dx^{m-1}} e^{-x^2} dx)
et ainsi de suite. Après n IPP
^{m+n} \int_{\R} H_n^{(n)}(x) \dfrac{d^{m-n} }{dx^{m-n}} e^{-x^2} dx=0)
(car m-n>0 et}(x) =)
cste )
Pour le 1.6
On reprend la dernière ligne du message précédent qui reste valable pour m=n d'où
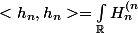}(x) e^{-x^2} dx=...)
On obtient le résultat avec l'aide de la question 1.x (x<5)
Et bien oui mais parfois il faut donner des nouvelles parce que ça prend du temps d'écrire.
Pour 1.5, m>n
une IPP donne
et ainsi de suite. Après n IPP
(car m-n>0 et
Pour le 1.6
On reprend la dernière ligne du message précédent qui reste valable pour m=n d'où
On obtient le résultat avec l'aide de la question 1.x (x<5)
Et bien oui mais parfois il faut donner des nouvelles parce que ça prend du temps d'écrire.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :