Calculer
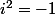
Cordialement,
Dacu
Un calcul
11 messages
- Page 1 sur 1
Re: Un calcul
par Sylviel » 19 Juin 2019, 08:59
Si x est réel il suffit d'utiliser l'exponentielle complexe.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Un calcul
par Dacu » 20 Juin 2019, 06:14
Dattier a écrit:Bonjour,
Bonne journée.
Bonjour,
Je ne comprend pas!Certains disent que ce n'est pas vrai que
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Un calcul
par Skullkid » 20 Juin 2019, 21:04
lyceen95 a écrit:ok sur ça aussi ?
Perso je suis pas ok si on ne me dit pas qui sont a et b... Comme d'habitude avec les posts de Dacu, la moitié des objets ne sont pas définis ou situés proprement.
Re: Un calcul
par Dacu » 21 Juin 2019, 06:38
lyceen95 a écrit:ok sur ça ?
Conclusion ....
Bonjour,
Êtes-vous sûr que
1) https://www.wolframalpha.com/input/?i=(cos(x%5E2)%2Bisin(x%5E2))%5Ex,x%3D2.1
2) https://www.wolframalpha.com/input/?i=cos(x%5E3)%2Bisin(x%5E3),x%3D2.1 ?!?!
Merci très beaucoup!
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Un calcul
par azertytreza » 21 Juin 2019, 06:49
Cette façon d'ignorer le message de Skullkid et de continuer à poser une question comme si tu n'avais pas vu ce qu'il te dit
ça s'appelle comment? ... la bêtise? ...le mépris?
ça s'appelle comment? ... la bêtise? ...le mépris?
Re: Un calcul
par Dacu » 21 Juin 2019, 07:29
azertytreza a écrit:Cette façon d'ignorer le message de Skullkid et de continuer à poser une question comme si tu n'avais pas vu ce qu'il te dit
ça s'appelle comment? ... la bêtise? ...le mépris?
Bonjour,
Ne pensez-vous pas qu'il serait préférable de répondre aux questions ci-dessous?
Comment expliquez-vous les résultats suivants de WolframAlpha:
1) https://www.wolframalpha.com/input/?i=(cos(x%5E2)%2Bisin(x%5E2))%5Ex,x%3D2.1
2) https://www.wolframalpha.com/input/?i=cos(x%5E3)%2Bisin(x%5E3),x%3D2.1 ?!?!
Merci très beaucoup!
Cordialement,
Dacu
Et DIEU dit :<<La lumière soit !>> Et la lumière fut.
Re: Un calcul
par Skullkid » 21 Juin 2019, 08:05
Tu ne nous as toujours pas dit où vivait x ni comment tu définis l'exponentiation...
En supposant que x est un complexe quelconque et en prenant la même définition que Wolfram Alpha pour l'exponentiation complexe (détermination principale du logarithme), alors^x = \exp\left(ix^3-2i\pi x \lceil \frac{\mathfrak{R}(x^2)-\pi}{2\pi}\rceil\right))
avec 
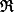
la partie réelle et 
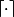
la partie entière supérieure.
En supposant que x est un complexe quelconque et en prenant la même définition que Wolfram Alpha pour l'exponentiation complexe (détermination principale du logarithme), alors
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :