On peut dire que l'intégrale existe car
est continue sur
J'ai
or,
=
Est ce suffisant, manque t'il quelques chose ?Merci
Encadrement,
2 messages
- Page 1 sur 1
encadrement,
par fastandmaths » 15 Juin 2019, 15:07
Bonjour,
| . \text { Montrer: }} \\ {\qquad\left|\int_{0}^{1}(f(x)+x f(x^2)) \mathrm{d} x\right| \leqslant \dfrac{3}{2} M}\end{array})
On peut dire que l'intégrale existe car+x f(x^2))
est continue sur 
.Comme
est continue sur le Sup existe aussi.
J'ai
+x f(x^2)) \mathrm{d} x\right| \leqslant \int_{0}^{1}|f(x)+x f(x^2)| \mathrm{d} x}{\leqslant \int_{0}^{1}(|f(x)|+x|f(x^2)|)\mathrm{d} x}\end{array})
or,|)dx+\int_{0}^{1}(x|f(x^2)|)dx \leqslant\int_{0}^{1}M(1+x) dx)
avec 
=
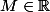
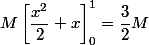
Est ce suffisant, manque t'il quelques chose ?Merci
On peut dire que l'intégrale existe car
est continue sur
J'ai
or,
=
Est ce suffisant, manque t'il quelques chose ?Merci
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :