Bonjour,
Quelqu'un pourrait-il m'aider à résoudre l'équation différentielle suivante :
dx/dt=k(0,01-x)^2
x est bien entendu la fonction, dx/dt=x' et t est la variable.
Merci à vous.
Equation différentielle
4 messages
- Page 1 sur 1
Re: Equation différentielle
Bonjour, tu peux résoudre ça à la physicienne :
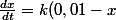^2\iff \frac{dx}{(0,01-x)^2}=k.dt)
Tu peux ensuite intégrer : avec
avec 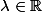 puis
puis  . Une condition initiale permettrait de trouver
. Une condition initiale permettrait de trouver  . S'il s'agit d'un problème physique tu peux rédiger comme ça, si en revanche il s'agit d'un problème de maths je te le déconseille (faute de rigueur).
. S'il s'agit d'un problème physique tu peux rédiger comme ça, si en revanche il s'agit d'un problème de maths je te le déconseille (faute de rigueur).
Tu peux ensuite intégrer :
Re: Equation différentielle
Il s'agit de l'étude d'une réaction chimique. la condition initiale est définie par x(0)=0.
Re: Equation différentielle
Merci "Tuvasbien" pour ta réponse.
la solution particulière est x(t)=(-1/kt+100)+0,01.
la solution particulière est x(t)=(-1/kt+100)+0,01.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
