Une partie de la frontière d'un ouvert
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Sarra_sonia
- Membre Naturel
- Messages: 66
- Enregistré le: 20 Jan 2015, 17:33
-
 par Sarra_sonia » 11 Juin 2019, 08:42
par Sarra_sonia » 11 Juin 2019, 08:42
Bonjour à tous,
Mon prof me dit que : "si on considère un ouvert

de

alors la partie de la frontière définie par
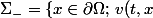 \cdot n(x) \leq 0 \})
peut se voir comme une variété de dimension

. "
où

est une fonction vectorielle définie sur
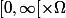
et
)
est la normale extérieure au point

.
Est-ce qu'il y a quelqu'un qui pet m'expliquer cette propriété?
Merci.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 11 Juin 2019, 08:50
par GaBuZoMeu » 11 Juin 2019, 08:50
Curieux. Ça demande tout de même quelques propriétés de régularité de

, ensuite
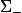
dépend de t, ensuite vu comme tu le formules
)
n'est pas défini sur la frontière de

, ensuite la supposée variété aura un bord etc.
Bref, éclaire-nous plus sur le contexte !
-
Sarra_sonia
- Membre Naturel
- Messages: 66
- Enregistré le: 20 Jan 2015, 17:33
-
 par Sarra_sonia » 11 Juin 2019, 09:03
par Sarra_sonia » 11 Juin 2019, 09:03
Oui vous avez raison, la fonction
)
est définie sur
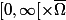
et appartient à l'espace
))
.
Pour la régularité de

il est muni d'une frontière de classe
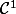
.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 11 Juin 2019, 12:09
par GaBuZoMeu » 11 Juin 2019, 12:09
Si
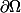
est

(de façon que

soit

), si
)
est

sur
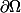
, et si

est une valeur régulière de
\cdot n(x))
, alors
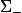
est une variété à bord de dimension

.
Après "peut se voir comme" n'est pas la même chose que "est". Je ne sais pas le sens précis à donner à "peut se voir comme". Ça dépend de ce qu'on fait avec
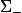
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités