Existence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 10 Juin 2019, 15:09
par mehdi-128 » 10 Juin 2019, 15:09
Bonjour,
Soit

une application de

dans

vérifiant :
 \implies \left ( \dfrac{f(x)-f(y)}{x-y} = \dfrac{f(x)-f(z)}{x-z} \right ))
Montrer l'assertion
 \in \R^2 \ \forall x \in \R \ f(x)=ax+b)
J'ai essayé l'analyse synthèse mais je trouve


-
aviateur
 par aviateur » 10 Juin 2019, 15:27
par aviateur » 10 Juin 2019, 15:27
Bonjour
Tu raisonnes et tu arrives à a=a. Mais comment tu as fait?
Sinon ton problème est vraiment simple: En effet si une telle fonction existe alors l'identité est vraie pour
x=0, y=1 et tout z. Alors tu peux exprimer f(z) et on voit apparaître la solution.
Tu peux rédiger maintenant
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 10 Juin 2019, 19:43
par mehdi-128 » 10 Juin 2019, 19:43
En remplaçant
)
par
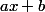
et
)
par
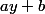
dans
-f(y)}{x-y} = \dfrac{f(x)-f(z)}{x-z})
Je trouve, en posant
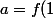-f(0))
et
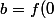)
 \implies a = \dfrac{f(z)-b}{z})
Mais comment faire si
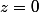
ou
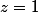

-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 10 Juin 2019, 20:30
par pascal16 » 10 Juin 2019, 20:30
si tu pars de la réponse, il est normal que le système te dise que c'est toujours vrai.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 10 Juin 2019, 20:43
par mehdi-128 » 10 Juin 2019, 20:43
D'accord merci.
Comment faire pour
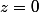
ou
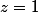
?
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 10 Juin 2019, 20:55
par pascal16 » 10 Juin 2019, 20:55
tu changes ta valeur de x car z=x est un cas déjà interdit dans l'énoncé.
Mais bon, dans ce sens là, c'est évident, les formules données calculent le taux d’accroissement entre deux points, et, du moment qu'on peut le calculer, il est constant pour une fonction type f(x)=ax+b.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 10 Juin 2019, 21:26
par GaBuZoMeu » 10 Juin 2019, 21:26
M'enfin ?
La formule quantifiée est vraie pour tout x et pour tout y. En particulier pour x=0 et y=1.
N'es-tu pas capable de remplacer x par 0 et y par 1 dans la formule quantifiée ?
Il te restera après encore un petit bout de travail à faire, tu obtiendras une belle identité pour tout z différent de 0.
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 10 Juin 2019, 22:48
par mehdi-128 » 10 Juin 2019, 22:48
Bah c'est ce que j'ai fait je trouve en posant
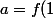-f(0))
et
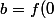)
 \implies a = \dfrac{f(z)-b}{z})
 \implies f(z)=az+b)
Mais je n'ai toujours pas compris comment faire quand
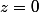
et
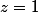
...
-
aviateur
 par aviateur » 10 Juin 2019, 23:19
par aviateur » 10 Juin 2019, 23:19
Si f est solution alors pour x=0 et y=1 et tout z différent
de 0 et 1 on a,,,,,,,,
continue maintenant le raisonnement

-
FLEURISTIN
- Membre Naturel
- Messages: 43
- Enregistré le: 03 Avr 2018, 15:54
- Localisation: Lorient (France)
-
 par FLEURISTIN » 11 Juin 2019, 00:33
par FLEURISTIN » 11 Juin 2019, 00:33
-
aviateur
 par aviateur » 11 Juin 2019, 09:13
par aviateur » 11 Juin 2019, 09:13
@fleuristin, Ah oui merci.
Il exagère
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités