Bonsoir à tous !
Je vous présente un problème que nous avons dû essayer de retranscrire sur le logiciel Scilab.
Voici l'énoncé :
> L'idée de ce projet est de considérer une expérience qui se répète indéfniment et d'attendre le
deuxième succès. Par exemple considérer un dé que l'on lance jusqu'à obtenir le six pour la deuxième
fois. Ou bien une pièce pipée qui fait Pile avec une probabilité p et d'attendre le deuxième Pile
(avec p < 0:5).
On peut ainsi si poser la question du rang moyen d'apparition de ce deuxième succès.
Cette expérience est à mettre en lien avec le cours sur les variables aléatoires discrètes et la loi
géométrique (loi du premier succès d'une expérience aléatoire que l'on répète.
Idées de recherches:
1. Programmer une telle expérience (dans le cas d'une pièce pipée avec une probabilité p en
paramètre)
2. Déterminer le rang moyen à partir duquel le deuxième Pile apparait
3. Combien de lancer faut il faire pour être certain (quasi certain) d'avoir ce deuxième succès?
4. Représentation graphique pertinente?
5. Etude théorique
J'ai réussi à programmer les 4 premières questions, malheureusement je me casse les dents depuis quelques jours sur la dernière qui doit être rédigée sur feuille et non sur le logiciel.
Voici mes quelques griffonnages qui me semblent être les plus cohérents :
On définit X= La rang du deuxième succès et Y=le rang du premier succès, Y est un VA qui suit la loi géométrique.
Si je cherche P(X=2) j'ai très simplement P(X=2)= P(Y1 inter Y2)
Le problème c'est que plus j'augmente mon rang plus les possibilités augmentent et je n'arrive pas à trouver une formule générale.
Je vous serais reconnaissant si vous pourriez me guider dans la résolution de cette dernière question.
Merci d'avance pour votre aide.
Cordialement.
Yugara
Problème de probabilité
3 messages
- Page 1 sur 1
Re: Problème de probabilité
Bonjour
Je ne comprends, C'est quoi Y1 et Y2?
Soit X la v.a qui représente le rang de l'arrivée du second succès et Y= le rang du premier succès.
pour
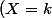=[(X=k).(Y=1)]+[(X=k).(Y=2)]+....+[(X=k).(Y=k-1)])
D'où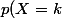= (k-1) q^{k-2} p^2)
et=\sum_{k=2}^\infty k (k-1) q^{k-2} p^2=2/p)
Je ne comprends, C'est quoi Y1 et Y2?
Soit X la v.a qui représente le rang de l'arrivée du second succès et Y= le rang du premier succès.
pour
D'où
et
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
