Bonjours , je dois étudier deux fonctions a 2 variable mais je bloque
Soit:
f(x,y)= xy² - ((e^2x) /2 ) +4x -y² + 3/2
g(x,y)= y ln(y) -2x * e^x
1) donner le domaine de définition de f et de g puis déterminer l'expression de leur dérivées partielles du premier et second ordre.
2) dans la perspective d'une identification d'éventuels extremums de la fonction f sous la contrainte de g(x,y)=0, vérifier que toutes les conditions nécessaire à l'utilisation de la méthode du multiplicateur de Lagrange sont réunies pour le point N(0,1)
Je remercie infiniment tout ceux qui pourrons m'apporter une aide ou une piste de réflexion
Fonction a deux variable
8 messages
- Page 1 sur 1
Re: fonction a deux variable
Je trouve que f(x,y) est définis sur R² et g(x,y) est définis sur R x R+
(ne trouvant aucun sujet similaire j'aimerais savoir si ces résultat sont correcte , merci )
(ne trouvant aucun sujet similaire j'aimerais savoir si ces résultat sont correcte , merci )
Re: fonction a deux variable
je trouve ensuite f'(x) =y²-e^2x +4 ---> quand je cherche pour le point N(0,1) je ne trouve pas un résultat égal a 0
et pour f'(y) je trouve f'(y)=2yx-2y le même problème , pour le point N(0,1) je trouve -2 et non pas 0 donc les conditions ne sont donc pas respecté ? merci pour vôtre aide
et pour f'(y) je trouve f'(y)=2yx-2y le même problème , pour le point N(0,1) je trouve -2 et non pas 0 donc les conditions ne sont donc pas respecté ? merci pour vôtre aide
Re: fonction a deux variable
Quand tu écris f'(x), tu veux dire "dérivée partielle de f par rapport à x" ? La notation est très malheureuse. Tant qu'à faire court, il vaut mieux écrire f_x.
La valeur que tu indiques pour f_x au point N n'est pas la bonne : tu t'es trompé dans ton calcul.
Ensuite, tu devrais revoir dans ton cours "les conditions nécessaires à l'utilisation de la méthode du multiplicateur de Lagrange". Ce n'est pas que les dérivées partielles de la fonction dont on cherche les extrema sous contrainte soit nulles !
La valeur que tu indiques pour f_x au point N n'est pas la bonne : tu t'es trompé dans ton calcul.
Ensuite, tu devrais revoir dans ton cours "les conditions nécessaires à l'utilisation de la méthode du multiplicateur de Lagrange". Ce n'est pas que les dérivées partielles de la fonction dont on cherche les extrema sous contrainte soit nulles !
Re: fonction a deux variable
Oui c'est exactement ce que je voulais dire par la , c'est la notation inscrite dans mon cours pourtant , je n'ai pas indiqué de valeur pour f_x j'ai simplement dis que je ne trouvé pas 0, je trouve "4 " après calcul.
très bien je vais revoir sa alors .
Mes dérivé partielle sont elle juste tout de même ? merci
très bien je vais revoir sa alors .
Mes dérivé partielle sont elle juste tout de même ? merci
Re: fonction a deux variable
Je n'arrive pas à croire que ton cours note f'(x) la dérivée partielle par rapport à x. Je n'ai encore jamais vu ça. La notation 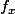 ou éventuellement
ou éventuellement  , je veux bien.
, je veux bien.
Pour la valeur de la dérivée partielle par rapport à x j'avais lu trop vite, excuse moi, je suis d'accord avec le 4 (et avec l'expression des dérivées partielles). Mais, je le répète, revois ton cours sur la méthode des multiplicateurs de Lagrange.
Pour la valeur de la dérivée partielle par rapport à x j'avais lu trop vite, excuse moi, je suis d'accord avec le 4 (et avec l'expression des dérivées partielles). Mais, je le répète, revois ton cours sur la méthode des multiplicateurs de Lagrange.
Re: fonction a deux variable
Oui en effet ..... tu a raison j'ai bien dans mon cours la deuxième notation que tu a inscrit je l'ai écris de la sorte car je ne suis pas très a l'aise sur ce forum et je ne sais tout simplement pas écrire le "petit x en bas " comme tu la fait .
Super merci pour les dérivées partielles ! c'est déjà un bon point pour moi qui ne suis pas très a l'aise avec sa !!
Très bien je retourne travailler , le problème si je me permet d'écrire sur ce forum c'est que mon cours est très pauvre a ce sujet et on me parle de maximum lié et maximum libre et je suis un peut perdue peut être pourriez-vous juste me dire si ce sont les même condition pour ces deux types de maximum ?
Sois je suis très nul en recherche sois je dois ben avoué que les information a ce sujet sont assez dur a trouvé.
Encore une fois merci infiniment de prendre le temps de m'aider .
Super merci pour les dérivées partielles ! c'est déjà un bon point pour moi qui ne suis pas très a l'aise avec sa !!
Très bien je retourne travailler , le problème si je me permet d'écrire sur ce forum c'est que mon cours est très pauvre a ce sujet et on me parle de maximum lié et maximum libre et je suis un peut perdue peut être pourriez-vous juste me dire si ce sont les même condition pour ces deux types de maximum ?
Sois je suis très nul en recherche sois je dois ben avoué que les information a ce sujet sont assez dur a trouvé.
Encore une fois merci infiniment de prendre le temps de m'aider .
Re: fonction a deux variable
La méthode des multiplicateurs de Lagrange pour les extrema liés doit tout de même être expliquée dans ton cours.
Tu peux éventuellement voir la page wikipedia.
Tu peux éventuellement voir la page wikipedia.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
