Bonjours a tous ,
Je dispose d'une fonction définie sur R de la forme f(x)->x-sin(x)
on me demande dans un premier temps de montré qu'elle n'admet PAS 2pi pour période , pour ce faire j'ai montré que f(pi) n'est pas égale a f(3pi)
Ensuite on me demande
b) Tirez cependant de la démonstration précédente, un principe permettant de réduire significativement le domaine d'étude de f . (je remarque que la même "forme" se répète tout les 2pi donc je suppose que on va pouvoir réduire sur [0,2pi] (sans grande conviction))
Puis,
c)Complétez, à partir d'une autre considération la réduction déjà obtenue du domaine d'étude de f.
Et la je suis complètement perdue...
merci pour vôtre aide si précieuse
Fonction trigo
8 messages
- Page 1 sur 1
Re: Fonction trigo
1°) ) = Quelque chose de simple où apparaît
= Quelque chose de simple où apparaît )
2°) À part la périodicité, quel genre de propriété est utile pour réduire le domaine d'étude d'une fonction ?
2°) À part la périodicité, quel genre de propriété est utile pour réduire le domaine d'étude d'une fonction ?
Re: Fonction trigo
J'ignoré qu'il exister d'autre propriété a ce sujet je vais chercher merci , pour la 1) la réponse est donc bien [0,2pi] ? merci
Re: Fonction trigo
Tu n'as pas complété le  = {?}) . C'est ça, le "principe" qui t'est demandé.
. C'est ça, le "principe" qui t'est demandé.
Ensuite : pourquoi peut-on réduire le domaine d'étude de de
de  à
à 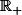 ?
?
Ensuite : pourquoi peut-on réduire le domaine d'étude de
Re: Fonction trigo
En effet je n'avais même pas compris que c'était une question que vous me posiez...
je dirais f(x+2pi)= f(x) +2pi
Ensuite , grâce au théorème des puissance comparé on sais que x^3 sera toujours supérieur a x donc le résultat sera forcément positif
je dirais f(x+2pi)= f(x) +2pi
Ensuite , grâce au théorème des puissance comparé on sais que x^3 sera toujours supérieur a x donc le résultat sera forcément positif
Re: Fonction trigo
J'ai dit une énorme bêtise , si le "x" est négatif le résultat sera négatif mais je pense cerner le problème , le résultat aura le même taux d'accroissement mais inversé dans les négatif que dans les positif (désolé si je n'utilise pas les bon terme ) ce que j'entend par la c'est que la courbe aura pour symétrie 0 , mais je ne connais absolument pas les formule qui permettrais d'appliquer ce raisonnement a mon exercice
Encore une fois je vous remercie de prendre le temps de m'aider
Encore une fois je vous remercie de prendre le temps de m'aider
Re: Fonction trigo
dwaldo a écrit:b) Tirez cependant de la démonstration précédente, un principe permettant de réduire significativement le domaine d'étude de f . (je remarque que la même "forme" se répète tout les 2pi donc je suppose que on va pouvoir réduire sur [0,2pi] (sans grande conviction))
oui, la courbe de f est invariante par la translation de vecteur
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 15 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
