Une bijection

[Aispor]

Bonjour, j'ai un peu de mal à montrer qu'une fonction est bijective.



Merci d'avance !

[aviateur]

Bonjour
Surement de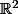 dans 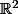tu veux dire?

Tout revient à résoudre l'équation

exp(x)-exp(y)=a et x+y=b.
Donc y=b-x
alors
exp(x)-exp (b-x)=a.

Pour cette dernière équation j'introduirai l'inconnue auxilliaire X=exp(x)....

Maintenant de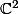 dans 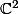c'est différent.

[Aispor]

Merci !