Probabilité

[bargain99]

Bonsoir,

Soit X et Y deux var ind suivant une loi de poisson de paramètres différents. Et Z= X+Y.

On me demande P(X=k | Z=n), je trouve ( dsl votre editeur d équation plante sur mon tel)

Sigma { [ ( k parmi n)* a^k*b (n-k)]/ (a+b)^n]}
Ou a et b les parametre des loi de X et Y.

Seulement ensuite en me demande :
Soit phi  (x) = E(X| Z= x) 
Calculez l'espérance et la variance de T= phi (Z). 

Et la je me retrouve devant sigma k*P(X=k | Z=n) que je ne.sait pas calculer. Biensur que ca fait penser a la loi binomiale,mais la somme des paramètres ne vaut pas 1... alors...

Merci d avance

[GaBuZoMeu]

Bizarre, il me semblait bien avoir vu dans ce fil une réponse d'aviateur où il écrivait entre autres que le "Sigma" n'avait rien à faire dans l'expression de P(X=k|Z=n).

C'est bien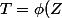 que tu voulais écrire ? Il ne reste plus que T= (Z).

[aviateur]

Il faut dire que tu mets un temps à répondre et que tu t'aperçois que la réponse est déjà donnée ailleurs!

[GaBuZoMeu]

Ah d'accord, tu as bien effacé ta réponse ; je n'avais pas halluciné, ça me rassure.

[bargain99]

Bonsoir,

Merci de vos réponses. J ai pas tout compris mais j ai trouvé, alors ^^

https://photos.app.goo.gl/NzWsaJWFjzR3NgAD6

Voila pr ceux qui passerons par ici et qui souhaiteraient la réponse.

Biz!