Différentielle exacte

[kennyuuuu]

Bonjour,
je bloque sur cette exercice je n'arrive pas à trouver a.

ax/y dx - x²/y² dy où a désigne une constante

a) Pour quelle valeur de a cette forme est -elle différentielle totale exacte.

b) Pour la valeur de a ainsi calculée , trouver la fonction F(x,y) dont ax/y dx -x²/y² dy est la forme différentielle totale.


Ce que j'ai fait :

a) df/dy (ay/y )= ax2y/(y²)² df/dx(- x²/y² dy)= 2x/y²

ax2y/(y²)² =2x/y²


a=x/y²

merci

[mathelot]

ay/y dx - x²/y² dy où a désigne une constante

Il y a une maladresse dans l'écriture de la forme différentielle. Pourquoi ay/y n'est pas simplifiée ?

[GaBuZoMeu]

Avec un petit plus de soin dans ce que tu fais, tu devrais y arriver.

Déjà l'énoncé de la question b montre que ta forme différentielle est

et pas ce que tu écris.

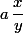
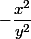
Ensuite, applique-toi en dérivant par rapport à et par rapport à .