Polynome et dérivée

[guillaume100]

Bonjour à tous,

Comment établir :



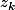
où les sont les racines de

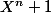
Est-ce que il y a un lien avec les ponynomes de tchebychev ?

Edit : la somme part de 1 et P est un polynome a coefficients complexes

[aviateur]

Bonjour
Déjà il faudrait savoir ce que c'est P (un polynôme? de quel degré?) et puis plus grave, il faudrait une formule qui a du sens. X^n+1 a n racines et dans ta formule il y en a n+1..

[GaBuZoMeu]

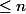
L'énoncé correct a pour hypothèse que est un polynôme de degré , et la somme porte sur les racines -èmes de l'unité, c'est bien ça ?

[GaBuZoMeu]

Pas de réaction.

Bon, une façon de démontrer l'affirmation (une fois correctement énoncée) consiste à considérer la somme des résidus de la fraction rationnelle



pour .

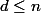
[guillaume100]

Bonjour, j'ai pris du temps a repondre j'avais oublié désolé

@aviateur : P est un polynome à coefficients complexes de degré quelquonque j'ai oublié de le préciser, je pense que la somme part de 1 dans l'énoncé

@GaBuZoMeu : Oui c'est ça la somme part de 1 dans l'enoncé et z0 n'existe pas, je vais éditer
Les résidus ce sont les éléments de la decomposition en éléments simples ?

[GaBuZoMeu]

P est un polynome à coefficients complexes de degré quelquonque

NON !!!! L'énoncé n'est valable que pour les polynômes de degré inférieur ou égal à !

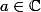
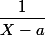
Le résidu en un pôle d'une fraction rationnelle est le coefficient de l'élément simple dans sa décomposition en éléments simples.

[guillaume100]

Ok j'admets que c'est de degré n, mais comment on en est sur que cela ne marche pas pour les autres polynomes ?



Et après pourquoi (1-X)^2 au dénominateur ?

Edit : la somme part de 1

[GaBuZoMeu]

Ok j'admets que c'est de degré n, mais comment on en est sur que cela ne marche pas pour les autres polynomes ?



Et après pourquoi (1-X)^2 au dénominateur ?

On est sûr parce qu'on peut voir des contre-exemples.
Tu fais encore une somme de 0 à n dans ta décomposition en éléments simples : répétition d'erreur !
Pourquoi le au dénominateur ? Pour retrouver le au dénominateur. Maintenant, il y a d'autres façons de le faire apparaître.

[guillaume100]

Ah ouais merci !

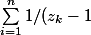=-n/2 parce que ça vaut P est scindé à racines simples

Comment faire apparaitre le dernier terme de l'egalité ?

Edit : il y a un moins devant n/2

[GaBuZoMeu]

Hum ... Là je ne te suis pas. Comment obtiens-tu cette égalité ? N'aurais-tu pas oublié quelque chose en cours de route ?

[guillaume100]

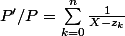
parce que P est scindé à racines simples et l'evaluation en 1 donne le resultat avec P=X^n+1

J'ai oublié un moins en cours de route dans le resultat precedent

[GaBuZoMeu]

Encore k de 0 à n ! Tu es incorrigible.
Sinon, OK. Mais le résultat que tu cherches ?