Lien entre séries formelles et fractions rationnelles
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lisitsa
- Messages: 9
- Enregistré le: 23 Déc 2018, 14:07
-
 par lisitsa » 25 Mai 2019, 21:43
par lisitsa » 25 Mai 2019, 21:43
Bonjour,
On sait que, étant donnée une fraction rationnelle
 = \frac{P(X)}{Q(X)} \in \mathbb{C}(X))
(avec

) et étant donné
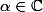
,

peut s'écrire sous la forme d'une série formelle
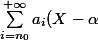^i}, \; a_i \in \mathbb{C})
(où

peut éventuellement être négatif).
Je dois monter que la réciproque est fausse, c'est-à-dire que toute série formelle ne provient pas d'une fraction rationnelle. Pour cela, on nous suggère de considérer les séries formelles
)
et
)
.
Mais je ne vois pas du tout comment faire...
Quelqu'un peut-il m'aider ?

Merci d'avance !
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Mai 2019, 09:33
par GaBuZoMeu » 26 Mai 2019, 09:33
Une fonction développable en série entière au voisinage de l'origine est caractérisée par sa série de Taylor à l'origine. Or l'exponentielle n'est pas une fraction rationnelle (considérer son comportement en

).
On peut aussi voir que le rayon de convergence de la série de Taylor d'un fraction rationnelle qui n'est pas un polynôme est forcément fini (penser aux pôles).
On peut encore voir que les coefficients de la série de Taylor d'une fraction rationnelle vérifient à partir d'un certain rang une récurrence linéaire d'ordre le degré du dénominateur.
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 26 Mai 2019, 13:05
par LB2 » 26 Mai 2019, 13:05
Ou encore (sous réserve) que la dérivée formelle de exp(X) est exp(X), donc si exp(X) était une fraction rationnelle, elle serait constante, car de degré -l'infini, car on a la propriété que deg(F') = deg F - 1 si F est une fraction rationnelle non constante.
-
lisitsa
- Messages: 9
- Enregistré le: 23 Déc 2018, 14:07
-
 par lisitsa » 26 Mai 2019, 18:25
par lisitsa » 26 Mai 2019, 18:25
Merci pour vos réponses.
GaBuZoMeu a écrit:Une fonction développable en série entière au voisinage de l'origine est caractérisée par sa série de Taylor à l'origine. Or l'exponentielle n'est pas une fraction rationnelle (considérer son comportement en

).
En quoi le comportement de la série exponentielle à l'infini l'empêche-t-il de provenir d'une série entière ?
LB2 a écrit:Ou encore (sous réserve) que la dérivée formelle de exp(X) est exp(X), donc si exp(X) était une fraction rationnelle, elle serait constante, car de degré -l'infini, car on a la propriété que deg(F') = deg F - 1 si F est une fraction rationnelle non constante.
Ce ne serait pas plutôt
 \leq \deg(F) - 1)
?
J'ai essayé de monter cette égalité, mais je n'obtiens qu'une inégalité (même si, en soit, je suis d'accord que ça empêche bien, malgré tout, la série exponentielle de venir d'une fraction rationnelle... Mais c'est juste pour être sûr).
Voici comment j'ai procédé :
Posons

,
=p, \; \deg(Q)=q)
. On a donc
=p-q)
.

,
= \deg(P')+\deg(Q)=p-1+q)
,
De même,
=q-1+p)
et
=2q)
.
D'où
 \leq p-1+q)
et donc
 \leq p-1+q-2q = p-q-1 = \deg (F)-1)
.
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 26 Mai 2019, 18:47
par LB2 » 26 Mai 2019, 18:47
Effectivement, a priori c'est seulement une inégalité large, je ne sais pas si ce que j'ai énoncé (deg(F') = deg(F)-1 est juste si F est non constante)
C'est clair si F est un polynôme, mais on pourrait envisager que des éléments simples de même degré, en dérivant, annulent le terme de degré deg(F)-1...
En tout cas l'inégalité large suffit pour montrer le résultat pour exp
L'égalité me semble vraie pour des éléments simples de première espèce, donc dans C(X). Ce qui m'étonne, c'est que je n'ai pas vu ce résultat (deg(F') = deg(F)-1 si F est non constante) dans la littérature, il a donc des chances d'être faux... mais je ne vois pas pourquoi, en tout cas en caractéristique nulle.
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 26 Mai 2019, 21:05
par GaBuZoMeu » 26 Mai 2019, 21:05
En quoi le comportement de la série exponentielle à l'infini l'empêche-t-il de provenir d'une série entière ?
Tu n'as sans doute pas écrit ce que tu voulais écrire.
L'exponentielle n'a pas la même croissance en $+\infty$ qu'une fraction rationnelle.
-
lisitsa
- Messages: 9
- Enregistré le: 23 Déc 2018, 14:07
-
 par lisitsa » 27 Mai 2019, 09:55
par lisitsa » 27 Mai 2019, 09:55
Ah, oui, effectivement, vu comme ça...
Je n'y avais pas pensé...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités

