Matrice
Olympiades mathématiques, énigmes et défis
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 13 Mai 2019, 00:08
par MMu » 13 Mai 2019, 00:08
Soit

une matrice

x

à coefficients réels telle que
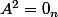
.
Montrer que pour

rééls et
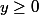
on a
\geq 0)
, où

est la matrice identité.


-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 13 Mai 2019, 08:22
par fatal_error » 13 Mai 2019, 08:22
hi,
Ajouter yI c'est juste shifter les vp de xA vers le haut
en représentant A sous forme triangulaire, les vp sont sur diago et le det prend le produit de la diago donc
rajouter lambdaI à A c'est juste rajouter lambda pour chaque vp de A
si X vecteur propre et h valeur propre de A
A^2X = AAX = AhX = h^2X et A^2 = 0 donc h = 0
donc toutes les vp de A sont nécessairement nulles et en fait
det(xA + yI) = produit des vp de A shifftées de y = y^n (!!)
la vie est une fête

-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 13 Mai 2019, 13:54
par GaBuZoMeu » 13 Mai 2019, 13:54
Le cas

ne présente pas grand intérêt et si
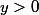
,
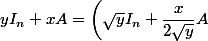 ^2\;.)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités

