Ptit souci........pa tro dur mé bon

[titi]

Voila bonjour à tous... Mq Z= (1+i)^2007-(1-i)^2007 est un imaginaire pur...

On me dit qu'il faut trouver 2i mais moi je trouve 4i...aidez moi svp

[Zebulon]

Bonsoir,
quelle est votre méthode ?

[boulay59]

Explique comment tu as fait, ...
pour info, je trouve 2^1004*i (au signe près, j'ai pas tout vérifié, ...)

[Zebulon]

pour info, je trouve 2^1004*i (au signe près, j'ai pas tout vérifié, ...)

Sûr ? Moi je trouve .

[boulay59]

En fait, je trouve -2^1004*i, et c'est mon dernier mot

[titi]

mé non mé 2007 c com ^3 c pareil alor c tou au lieu de faire le calcul avc ^2007 onle fé avc ^3....

[Zebulon]

mé non mé 2007 c com ^3 c pareil alor c tou au lieu de faire le calcul avc ^2007 onle fé avc ^3....

??
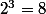
, alors que ?

[titi]

j'ai fait comme ça : (1+i)^2007-(1+i)^2007
équivaut : (1+i)^3-(1+i)^3
après calcul : = 4i mais tout le monde me dit qu 'ils ont trouvé 2i :@ je comprends pas

[Quidam]

En fait, je trouve -2^1004*i, et c'est mon dernier mot

Bon, les enchères sont ouvertes : moi aussi je trouve

Mais une erreur est si vite arrivée...

[Zebulon]

Bon, les enchères sont ouvertes : moi aussi je trouve

Mais une erreur est si vite arrivée...

J'ai pourtant une racine qui ne s'élève pas au carré... J'ai beau vérifier... Ceci dit, je suis tellement nulle en calculs !

[titi]

pourrais t-on m'expliquer mdrrrrr....

[Zebulon]

Indication : passer en écriture exponentielle.

[titi]

Mais non n'importe quoi......!!!!! Je comprends rien en fait je crois due vous non plus vous comprenez pas ma question lol....je réexplique en fait il fait montrer que le nombre précéden est un imaginaire pur je suis en terminale S et c'est sur les nombres complexes donc il faut résoudre ça avec des propriétés suremnt reprenez mon dernier message et regarder comment j'ai fait et dites moi si cela vous parez juste ou pas...

[BQss]

Mais non n'importe quoi......!!!!! Je comprends rien en fait je crois due vous non plus vous comprenez pas ma question lol....je réexplique en fait il fait montrer que le nombre précéden est un imaginaire pur je suis en terminale S et c'est sur les nombres complexes donc il faut résoudre ça avec des propriétés suremnt reprenez mon dernier message et regarder comment j'ai fait et dites moi si cela vous parez juste ou pas...

Calme toi:

deja on passe en exponentielle:

rac(2) (exp(iPi/4)-exp(-iPI/4))
Or d'apres la formule de moivre exp(iPi/4)-exp(-iPI/4)=2isin(PI/4)=2irac(2)/2

donc on trouve bien 2i


Maintenant tu fais la meme methode mais avec la puissance.

rac(2)^2007 *(exp(2007iPi/4)-exp(-2007iPI/4))=rac(2)^2007(exp(-iPi/4)-exp(2007iPI/4))=
rac(2)^2007(-2isin(Pi/4))=rac(2)^2007(-2isin(Pi/4))=[-rac(2)^2008]i=[-2^1004]i

qui est bien un imaginaire pur.

[BQss]

j'ai fait comme ça : (1+i)^2007-(1-i)^2007
équivaut : (1+i)^3-(1-i)^3
après calcul : = 4i mais tout le monde me dit qu 'ils ont trouvé 2i :@ je comprends pas

ils ont trouvé 2i sans elevé a la puissance, c'est qu'ils ont faux ou que ta question est fausse.
Mais en tout cas, c'est effectivement un imaginaire pur.

j'ai fait comme ça : (1+i)^2007-(1-i)^2007
équivaut : (1+i)^3-(1-i)^3

et cette equivalence est fausse.

Par contre on a:
(1+i)^(2n+1)=(-2)^[n] * (i)^(n+1) ou - cette expression periodiquement tout les 4n

[Gato]

hello , tu n'as pas besoin de calculer ce nombre puisque l'on demande juste de prouver qu'il est imaginaire pur.

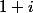
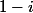
et étant conjugués , et le sont aussi;leur différence est donc un imaginaire pur.