Arithmétique ( Niveau Terminale)

[Hanaconda]

Bonsoir,
Svp j'ai besoin d'aide (solutions ou pistes ) pour l'exercice suivant ( niveau terminale)

Merci beaucoup d'avance.

[infernaleur]

Salut,

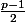
La première question qu'il faut se poser déjà c'est est-ce que est entier ? (a toi de trouver la réponse).

Ensuite pour la 1) le théorème qu'il faut utiliser dit que :

Donc

Or :


....


Maintenant je pense que tu peux réussir la question 1) et la question 2) aussi qui est plus simple

[infernaleur]

petite erreur je voulais écrire :


" Donc "

[Hanaconda]

(p -1)/2 est évidemment un entier, puisque p est impair, donc p-1 est pair donc 2 divise p-1.
Mais ce que je n arrive pas à capter c est pourquoi est-ce qu'on a (p-1)/2 et (p+1)/2 dans l'expression de (p-1)! ?
Serait-ce parce que 1 =< (p-1)/2 =< p-1 et (p-1)/2 un entier? Et il va de même pour (p+1)/2?

Merci infiniment!

[infernaleur]

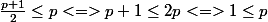
Donc comme p est plus grand que 1 tu as bien .
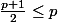
Tu peux t'amuser a montrer les autres inégalités si tu n'es toujours pas convaincue .

[infernaleur]

(p -1)/2 est évidemment un entier, puisque p est impair, donc p-1 est pair donc 2 divise p-1.
Mais ce que je n arrive pas à capter c est pourquoi est-ce qu'on a (p-1)/2 et (p+1)/2 dans l'expression de (p-1)! ?
Serait-ce parce que 1 =< (p-1)/2 =< p-1 et (p-1)/2 un entier? Et il va de même pour (p+1)/2?

Merci infiniment!

Donc oui c'est pour ça.

[Hanaconda]

Merci beaucoup.
Svp, des idées pour la 3ème question?

[infernaleur]

Combien y’a t-il d’elements de E^2 ?
Combien y’a t’il de restes possible dans la division euclidienne par p ?