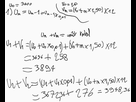Produit scalaire et suites

[PhilipeHook]

Bonjour,

Je suis en 1°S et je fais face à deux exos que je ne sais pas comment réoudre, l'un sur le produit scalaire et l'autre sur les suites.



et



Pour le premier j'ai déjà fais une des manière de calculer le produit scalaire mais je ne sais pas laquelle autre utiliser ni comment faire le reste de l'exercice.




Et pour le second je ne comprend pas comment faire la 2) b) ainsi que la 3).



Merci d'avance.

[PhilipeHook]

Petite erreur désolé

[hdci]

Bonjour,
Déjà dans ton produit scalaire il y a une erreur. Je ne sais pas d'où vient ta formule, mais le produit scalaire est égal au produit des modules multiplié par le cosinus de l'angle. Et avec cette "première" façon, on a une formule avec une inconnue, le cosinus de l'angle.

Pour la seconde façon : c'est avec les coordonnées. Le produit scalaire de deux vecteurs, c'est la somme du produit des abscisses et du produit des ordonnées. Il faut donc prendre une repère orthonormé astucieux (au hasard, A est au centre du repère, B est sur l'axe des abscisses...) et calculer les coordonnées de C ; sachant que C est sur le cercle de centre A et de rayon 10, et sur le cercle de centre B et de rayon 12. Ainsi, tu calcule très précisément la valeur du produit scalaire. On en tire cosinus de l'angle, puis l'angle.

Remarque : utilise un outil comme Geogebra pour vérifier : tu verras que le produit scalaire n'est pas égal à 96 mais à 54.

[hdci]

J'imagine que ton début de réponse, c'est la question 3. Commençons par regarder la 2-b).

Quelques sous-questions : quand on augmente une valeur de , est-ce que cela ne revient pas à multiplier cette valeur par un certain coefficient ? Quelle est alors ce coefficient ? (si tu ne connais pas la formule du coefficient, tu la retrouves facilement avec une factorisation).

Dès lors, la suite n'est-elle pas une suite où on multiplie chaque terme par ce coefficient pour calculer le terme suivant ? Comment s'appelle une telle suite ? Et dans ce cas, quelle est la définition explicite (par opposition à la relation de récurrence) ? Avec cela tu as exprimé en fonction de .

Enfin, n'est-elle pas une suite où on ajoute une même valeur pour passer d'un terme à son suivant ? Comment s'appelle une telle suite ? Quelle est sa définition explicite ?

Il n'y a plus qu'à remplacer par le rang de l'année 2030 (sachant que le rang 0 c'est l'année 2019).

Pour la question 3
Dans ce que tu as écrit, tu multiplies bien les charges par 12, mais pas le loyer ! Revois vite ce calcul !

Pour calculer et en fonction de et de , c'est assez évident. D'où, obtenir et en fonction de ...

Pour la 3-c, il suffit juste de voire qu'on fait une somme de termes de suites bien connues. Tu as dans ton cours les formules qui donnent la valeur de ces sommes en fonction de . Il n'y a plus qu'à prendre

[PhilipeHook]

Merci pour ta réponse.

Alors en fait cette formule me viens tout droit de mon cours



Et oui il smblerais bien que je me sois trompé, vu que l'angle que je trouve est 0°.
Mais du coup je ne vois pas comment faire (je ne comprend pas vraiment ce tu as au niveau de la "première méthode")

Et je ne vois pas comment faire pour calculer les coordonnées de C ni quelle méthode utilisé après (projection orthogonal peut être ?).


Et pour ce qui est du deuxième exercice, il s'agit en réalité de la question 1). Il s'agirait donc du début de réponse à la 3) , mais du coup, si ce n'est pas ça, comment répondre à la 1) ?


En ce qui concere la suite,
Je n'ai pas vraiment compris à propos de (Ln)
Quand tu parle de coefficient, s'agit t-il bien de Un=2n²-1
C'est donc une suite définie par une formule explicite.

(Ln) est une suite arithmétique de raison r tel que Un = U0 + nr

J'ai revu mon calcul (ayant en effet mal compris l'énoncé) mais je ne sais toujours pas pour quel question il sert en fin de compte.

[hdci]

Pour le premier exercice : tu fais une erreur quand tu calcules : la norme d'une somme de deux vecteurs, ce n'est en général pas du tout la somme des normes.
En l'occurrence, (par la relation de Chasles).

Donc et ce n'est pas du tout égal à 4.
Tu peux refaire le calcul avec cela.

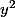
On trouve le même résultat qu'en cherchant les coordonnées du point . Donc inutile de les trouver, mais sinon, l'idée est de dire que est dans le repère orthonormé que j'ai mentionné puis de dire que AC=10, soit en élevant au carré, ; ensuite, BC=12, donc . En soustrayant les deux égalités, on élimine et il reste ce qui donne x=\dfrac{5}{4}, ce qui suffit pour calculer le produit scalaire (inutile de calculer y, car il va être multiplié par zéro).

En fait ça c'était la "seconde méthode" (ou la troisième).
La première méthode est celle-ci : si est l'angle formé par les vecteurs et



Pour le second exercice : tout d'abord,

Quand tu parle de coefficient, s'agit t-il bien de Un=2n²-1

Absolument pas et je ne vois pas d'où sors ce
Reprenons l'histoire du coefficient.
Quand tu augmentes une quantité de 10%, tu obtiens
Qu'obtiens-tu si tu factorise ? Tu obtiens Q multiplié par (...) qui est le coefficient dont je parle.
Et si au lieu de 10%, c'était 30% ? 1% ? un pourcentage quelconque p ?

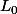
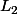
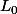
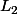
Reprends alors : que vaut ? Que vaut ? Que vaut ? Comment passes-tu de à ? de à ? Si tu penses que c'est une suite arithmétique, alors c'est que tu ajoutes toujours la même constante, mais est-ce le cas ?

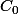
Pour les charges, comment passe-t-on de à , puis de à , etc. ?

[PhilipeHook]

Merci beaucoup pour ton aide, j'ai réussi le première exercice mais en ce qui concerne le deuxième je ne vois pas comment trouver l'expression générale de (Un) (aussi appelé (exprimer en fonction de n)/(forme explicite) au cas où, histoire d'être sur de quoi on parle). Ce qui me bloque pour la suite.

[hdci]

Je ne sais pas pourquoi dans mon message j'ai un cadre rouge avec le texte "can't mkdir cgi-bin" etc.

Ceci dit, tu as trouvé que était une suite géométrique et une suite arithmétique. Mais tu dis que la raison est et ça je ne comprends pas très bien d'où tu sors cela.

Si est une suite géométrique, que vaut en fonction de ? Quelle est la valeur de la raison ?
Ensuite, quelle est la valeur de ? Donc quelle est la valeur de en fonction de L_0 et de n ?
(En fait, j'ai l'impression que tu n'as pas bien compris la relation entre "une augmentation de x%" et "le coefficient multiplicateur d'une augmentation". Me trompe-je ?)