Applications linéaires

[Este]

Bonjour,
Je dois montrer que la fonction qui va de Cn[x] dans C[x], P : f(P)= P(x-a) + P(X-b) avec a,b deux complexes non égaux
est bijective
Etant donné l'egalité des dimensions des espaces d'arrivée et de depert il suffit de montré qu'elle injective ou surjective, mais je n'arrive pas a montré k'une de ces deux propriété.
Je voulais monter que ker f est reduit a 0 mais en prenant un P appartenant a ker f je me retrouve avec
P(X-a) + P(x-b)=0 et je ne vois pas comment montré que P est nul.

[noobey]

Ecris simplement les choses :
On suppose que P est différent de 0. Soit p son degré, alors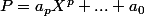 et


Et en identifiant les parties de degré p des deux côtés...

[Este]

J'avais pensé a faire cela, en effet comme les "degré" de chaque membre de la somme sont 2 à 2 distincts, on a
pour tout k, ak=0 ou (X-a)**k+(X-b)**k=0
Mais comment peut on affirmer que se ont les ak qui sont nuls et pas (X-a)**k+(X-b)**k

[noobey]

Identifie juste pour linstant le coeff de plus haut degré dans les 2 membres

[tournesol]

f est bijective de C[X] sur C[X]
En effet :
f conserve le degré .
Donc l'image de la base canonique de C[X] est de degrès échelonnés .
Or toute famille de degrés échelonnés est une base de C[X] .
Donc l'image de la base canonique de C[X] est une base de C[X]
Or f est linéaire .
Donc f est bijective de C[X] sur C[X]
La conservation du degré entraine que f est bijective de Cn[X] sur Cn[X]