Limite avec ln
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
fab_92
- Membre Naturel
- Messages: 27
- Enregistré le: 12 Nov 2006, 19:11
-
 par fab_92 » 16 Nov 2006, 22:08
par fab_92 » 16 Nov 2006, 22:08
Bonsoir,voila la chose:

2xln(x+
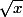
)
Merci d'avance.
-
flaja
- Membre Rationnel
- Messages: 904
- Enregistré le: 02 Juil 2006, 16:24
-
 par flaja » 16 Nov 2006, 23:30
par flaja » 16 Nov 2006, 23:30
bonsoir,
si on faisait le changement de variable : y = sqrt(x) ?
-
fab_92
- Membre Naturel
- Messages: 27
- Enregistré le: 12 Nov 2006, 19:11
-
 par fab_92 » 17 Nov 2006, 00:01
par fab_92 » 17 Nov 2006, 00:01
Que veux-tu dire?
-
boulay59
- Membre Naturel
- Messages: 92
- Enregistré le: 16 Oct 2005, 23:39
-
 par boulay59 » 17 Nov 2006, 00:11
par boulay59 » 17 Nov 2006, 00:11
Bah tu pose
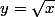
alors la limite de x en 0+ correspond à la limite de y en 0 de 2y²ln(y²+y)
-
fab_92
- Membre Naturel
- Messages: 27
- Enregistré le: 12 Nov 2006, 19:11
-
 par fab_92 » 17 Nov 2006, 00:17
par fab_92 » 17 Nov 2006, 00:17
D'accord, mais çà donne toujours une forme indéterminée non?
-
fab_92
- Membre Naturel
- Messages: 27
- Enregistré le: 12 Nov 2006, 19:11
-
 par fab_92 » 17 Nov 2006, 01:07
par fab_92 » 17 Nov 2006, 01:07
J'ai dit une connerie?
-
fab_92
- Membre Naturel
- Messages: 27
- Enregistré le: 12 Nov 2006, 19:11
-
 par fab_92 » 17 Nov 2006, 08:36
par fab_92 » 17 Nov 2006, 08:36
ou alors, ça fait 0-; j'ai bon? :++: ou pas? :briques:
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 17 Nov 2006, 08:48
par fonfon » 17 Nov 2006, 08:48
Salut, si c'est bien
})
alors oui la limite en 0+ est bien 0
-
fab_92
- Membre Naturel
- Messages: 27
- Enregistré le: 12 Nov 2006, 19:11
-
 par fab_92 » 17 Nov 2006, 08:56
par fab_92 » 17 Nov 2006, 08:56
Peux-tu détailler,stp?
-
johnjohnjohn
- Membre Rationnel
- Messages: 843
- Enregistré le: 24 Oct 2006, 11:00
-
 par johnjohnjohn » 17 Nov 2006, 09:47
par johnjohnjohn » 17 Nov 2006, 09:47
fab_92 a écrit:Peux-tu détailler,stp?
Alors sous toute réserve du droit d'utiliser la formule suivante en terminale :

=r.ln(a)\)
T'as donc pour tout x>0
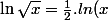\)
car

pour tout x>=0
et comme d'autre part tu sais par coeur que :
=0)
Alors la limite de la fonction demandée ne devrait plus te poser problème ...
-
johnjohnjohn
- Membre Rationnel
- Messages: 843
- Enregistré le: 24 Oct 2006, 11:00
-
 par johnjohnjohn » 17 Nov 2006, 11:37
par johnjohnjohn » 17 Nov 2006, 11:37
johnjohnjohn a écrit:Alors sous toute réserve du droit d'utiliser la formule suivante en terminale :

=r.ln(a)\)
T'as donc pour tout x>0
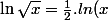\)
car

pour tout x>=0
et comme d'autre part tu sais par coeur que :
=0)
Alors la limite de la fonction demandée ne devrait plus te poser problème ...
Bon j'ai encore raconté des conneries. Ne tiens pas compte de mon message ....
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 17 Nov 2006, 13:04
par fonfon » 17 Nov 2006, 13:04
fab_92 a écrit:Peux-tu détailler,stp?
comme on te l'a déjà dit tu poses

donc

donc on obtient comme nouvelle limite:
})
or
}=2y^2ln(y(y+1))=2y^2ln(y)+2y^2ln(y+1))
je te laisse terminer
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 17 Nov 2006, 13:08
par fonfon » 17 Nov 2006, 13:08
fab_92 a écrit:Peux-tu détailler,stp?
comme on te l'a déjà dit tu poses

donc

donc on obtient comme nouvelle limite:
})
or
}=2y^2ln(y(y+1))=....)
je te laisse terminer
-
boulay59
- Membre Naturel
- Messages: 92
- Enregistré le: 16 Oct 2005, 23:39
-
 par boulay59 » 17 Nov 2006, 17:47
par boulay59 » 17 Nov 2006, 17:47
En fait, votre changement de variable ne sert à rien, il complique même les choses : tu as
)
:
- tu factorises dans le logarithme par le
terme dominant, idée à retenir !! (attention, on est en 0, le terme dominant, c'est
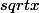
)
- tu sépares le produit en somme et le tour est (presque) joué
(tu obtiens en fait
 = x ln(x) + 2x ln(1+ \sqrt x))
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 17 Nov 2006, 17:52
par fonfon » 17 Nov 2006, 17:52
Salut boulay59, moi j'ai repondu avec le changement de variable car vous étiez 2 à le proposer
-
boulay59
- Membre Naturel
- Messages: 92
- Enregistré le: 16 Oct 2005, 23:39
-
 par boulay59 » 17 Nov 2006, 17:56
par boulay59 » 17 Nov 2006, 17:56
Je sais bien, mais je lui expliquait juste ce qu'était un changement de variables, (j'avais pas trop regardé l'exercice), mais là les réponses sont parties un peu en cacahuète.
Mais c'est vrai, je l'admets, j'aurais du dire NOTRE changement de variables ne sert à rien :happy2:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités

car
pour tout x>=0
) :
: 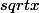 )
) = x ln(x) + 2x ln(1+ \sqrt x))
