Oui de toute façon il me semble que @pascal à fait un programme. Donc on peut vérifier avec plusieurs exemples la validité ou non des 2 formules.
Maintenant j'ai l'impression que tu essayes de trouver la formule qui va bien.
Mais moi c'est "presque" certain que c'est une démo, faite un peu à la va vite donc il faudrait la vérifier en détail.
Grosso modo j'ai partitionné le nombre de cas en fonction de la première fois où il va manquer de la monnaie.
Avec ton dessin c'est très pratique pour comprendre mon idée. Chaque élément de la partition correspond
à une trajectoire qui passe pour la première par un point juste en dessous de la diagonale (un point sur la droite y=x-1). C'est pour ça que j'ai une somme k qui va de 0 à 6 (en fait de 6 à 0).
Pour chaque k j'ai obtenu le nombre sous la forme d'un produit (je ne l'ai pas conservé en mémoire mais un des 2 termes est immédiat, l'autre un peu moins) ensuite j'ai simplifié. C'est pour cela que ta formule me semble plausible car on a une somme de k=0 à 6 et un produit que j'avais avant simplification. Mais la façon de compter n'est pas la même.
faire mais je comptais que je m'en assure.
Une chose est sûre j'ai
Permutation avec répétition
25 messages
- Page 2 sur 2 - 1, 2
Re: Permutation avec répétition
Comme je l'ai mis plus haut, ça revient sans doute au même.
J'ai partitionné en fonction du premier point d'entrée à l'intérieur de la zone verte, moi aussi.
Ta formule est plus simple
J'ai partitionné en fonction du premier point d'entrée à l'intérieur de la zone verte, moi aussi.
Ta formule est plus simple
Re: Permutation avec répétition
Salut,
En général, la méthode considérée comme "la plus jolie" pour dénombrer ce truc, c'est ce qu'on apelle "le principe de reflexion".
Et le dessin qu'on fait, c'est plutôt en metant en abscise le temps et en ordonné le nombre de billets de 5 Euros.
Ce faisant, chaque "pas", c'est une diagonale soit de (+1,+1), soit de (+1,-1).
S'il y a au départ personnes avec un billet de 5 et
personnes avec un billet de 5 et  avec un billet de 10 (avec
avec un billet de 10 (avec 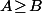 ,) c'est qu'on part du point
,) c'est qu'on part du point ) pour arriver au point
pour arriver au point ) .
.
Bien sûr, le nombre de trajets possible est le coefficient binomial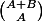 et ce qu'on veut dénombrer, c'est la nombre de tels trajets qui restent tout le temps au dessus (au sens large) de l'axe des
et ce qu'on veut dénombrer, c'est la nombre de tels trajets qui restent tout le temps au dessus (au sens large) de l'axe des  .
.
Or, si on prend un trajet qui passe en dessous de l'axe des , donc qui passe au moins une fois par un point
, donc qui passe au moins une fois par un point ) et qu'on lui associe le trajet obtenu en prenant le symétrique par rapport à la droite
et qu'on lui associe le trajet obtenu en prenant le symétrique par rapport à la droite 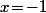 de toute la fin du parcours (tout ce qu'il y a après le premier point
de toute la fin du parcours (tout ce qu'il y a après le premier point ) du trajet), alors on obtient un nouveau trajet part du point
du trajet), alors on obtient un nouveau trajet part du point ) pour arriver au point
pour arriver au point ) .
.
Alors on voit clairement qu'il y a une bijetion entre :
- L'ensemble des trajets de) à
à ) passant au moins une fois en dessous de l'axe des
passant au moins une fois en dessous de l'axe des  .
.
- L'ensemble des trajets quelconques de) à
à ) .
.
Et évidement, le nombre de tels trajets, ben c'est le coefficient binomial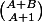 vu qu'il faut monter
vu qu'il faut monter 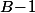 fois et descendre
fois et descendre 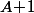 fois.
fois.
Bilan : la proba de ne pas avoir assez de billet de 5 Euros, c'est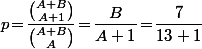 dans cet exo.
dans cet exo.
En général, la méthode considérée comme "la plus jolie" pour dénombrer ce truc, c'est ce qu'on apelle "le principe de reflexion".
Et le dessin qu'on fait, c'est plutôt en metant en abscise le temps et en ordonné le nombre de billets de 5 Euros.
Ce faisant, chaque "pas", c'est une diagonale soit de (+1,+1), soit de (+1,-1).
S'il y a au départ
Bien sûr, le nombre de trajets possible est le coefficient binomial
Or, si on prend un trajet qui passe en dessous de l'axe des
Alors on voit clairement qu'il y a une bijetion entre :
- L'ensemble des trajets de
- L'ensemble des trajets quelconques de
Et évidement, le nombre de tels trajets, ben c'est le coefficient binomial
Bilan : la proba de ne pas avoir assez de billet de 5 Euros, c'est
Modifié en dernier par Ben314 le 23 Avr 2019, 05:09, modifié 3 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Permutation avec répétition
Merci, ça a l'air plus simple. Je vais y regarder.
La formule de Pascal permet de passer facilement du résultat de Ben314 au résultat d'aviateur.
La formule de Pascal permet de passer facilement du résultat de Ben314 au résultat d'aviateur.
Re: Permutation avec répétition
Une dernière(?) contribution pour ce sujet.

Au vu des messages précédents, on pouvait raisonner avec la même grille. (idée d'@aviateur au départ, je crois)
Le nombre de chemins pour aller de A à B en entrant dans la zone verte est égal au nombre de chemins pour aller de A à C, le point C étant le symétrique de B par rapport à la droite en pointillés.
Ce nombre est donc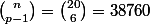
Proba pour que la monnaie puisse être rendue:
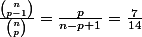

Au vu des messages précédents, on pouvait raisonner avec la même grille. (idée d'@aviateur au départ, je crois)
Le nombre de chemins pour aller de A à B en entrant dans la zone verte est égal au nombre de chemins pour aller de A à C, le point C étant le symétrique de B par rapport à la droite en pointillés.
Ce nombre est donc
Proba pour que la monnaie puisse être rendue:
25 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : SuperPoule et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
