Bonjour,
Je suis bloqué dans l'avant-dernière question de mon DM. Je vous résume rapidement ce que j'ai déjà fait avant de vous poser ma question.
Dans une première question j'ai étudié les matrices A carrées d'ordre n de la forme UtV (où tV est la transposée de V, je n'arrive plus à mettre le "t" en haut...) où U et V sont des matrices de dimension n,1. J'ai montré que ces matrices A sont de rang 1 si U et V sont toutes les 2 non nulles.
Puis dans une 2è question, j'ai étudié la réciproque en montrant que toute matrice A de rang 1 se met sous la forme XtY, où X et Y sont des matrices non nuls de Mn,1(K).
Dans la 3è question, j'ai commencé par montrer que si A est une matrice carrée de rang r alors il existe 2 familles libres (X1,,...Xr) et (Y1, ... ,Yr) de Mn,1(K) telles que A = la somme de i allant de 1 à r des XitYi.
Puis je dois démontrer la réciproque, à savoir si (X1, ... ,Xr) et (Y1, ... ,Yr) sont 2 famille libres de Mn,1(K) alors A qui est la somme des XitYi est de rang r. Et c'est cette question que je n'arrive pas à faire.
J'ai commencé par dire que pour tout i, d'après la première question, le rang de XitYi est 1 puisque les familles étant libres les Xi et les Yi sont forcément tous non nuls .
Peut-on en déduire que le rang de A est inférieur ou égal à r? (en d'autres termes a-t-on le rang d'une somme qui est inférieur ou égal à la somme des rangs?).
Si cela était vrai il faudrait ensuite que je raisonne par l'absurde et que je suppose que e rang de A est strictement plus petit que r et que j'arrive à montrer une contradiction....
Merci d'avance si vous pouvez m'aider.
DM sur les matrices de rang r
6 messages
- Page 1 sur 1
Re: DM sur les matrices de rang r
Bonjour
Je ne sais pas comment tu as fait pour la proposition directe. (car je ne l'ai pas fait mais je me demande si la réciproque n'est pas cachée dans la démonstration directe).
Mais bon pour la réciproque.
Tu as Ce qui veut dire que les colonnes de M sont des combinaisons linéaires des
Ce qui veut dire que les colonnes de M sont des combinaisons linéaires des  . On en déduit que le rang colonne (dont le rang) de M est inférieur ou égal à r.
. On en déduit que le rang colonne (dont le rang) de M est inférieur ou égal à r.
Maintenant les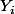 sont indépendants donc
sont indépendants donc ) est de dimension r.
est de dimension r.
Sans restreindre la généralité, considérons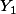 et son projeté orthogonal sur le sev de dimension n-1 de E_Y égal à
et son projeté orthogonal sur le sev de dimension n-1 de E_Y égal à ) . Soit
. Soit  ce vecteur et
ce vecteur et 
On a alors X_1)
et\neq 0.) Ce qui montre que
Ce qui montre que  est dans l'image de M. Mais de même
est dans l'image de M. Mais de même 
Le rg de M est donc égal à r.
PS j'ai mis les transposées à droite du vecteur.
Je ne sais pas comment tu as fait pour la proposition directe. (car je ne l'ai pas fait mais je me demande si la réciproque n'est pas cachée dans la démonstration directe).
Mais bon pour la réciproque.
Tu as
Maintenant les
Sans restreindre la généralité, considérons
On a alors
et
Le rg de M est donc égal à r.
PS j'ai mis les transposées à droite du vecteur.
Re: DM sur les matrices de rang r
Déjà merci beaucoup!
Est-ce que X1(Y1tY1)=(tY1Y1)X1 parce que tY1Y1 peut être assimilé à un nombre?
Pour le sens direct j'ai utilisé un résultat du cours qui dit que toute matrice de rang r est semblable à Jr qui est la matrice carrée avec des zéros presque partout sauf sur les r premiers éléments de la diagonale. J'ai donc dit qu'il existe 2 matrices carrés inversibles P et Q telles que A=QJrP. Puis j'ai écrit Jr sous la forme Jr= sigma de 1 à r des EitEi, où (Ei ) est la base canonique de Mn,1(K). A la fin j'ai posé Xi=QEi et Yi=tPEi. Pour finir j'ai montré que les 2 familles étaient libres.
Pour finir cet exercice, je dois montrer que si (X1, ... , Xn) et (Y1, ... , Yn) sont 2 bases de Mn,1(K), alors la famille (XitYj) est une base de Mn(K).
En fait c'est une famille de nxn éléments qui est la dimension de Mn(K).
Il me reste à utiliser le 3è pour montrer que c'est une famille génératrice de Mn(K). Et je pourrai conclure.
Je cherche...
Est-ce que X1(Y1tY1)=(tY1Y1)X1 parce que tY1Y1 peut être assimilé à un nombre?
Pour le sens direct j'ai utilisé un résultat du cours qui dit que toute matrice de rang r est semblable à Jr qui est la matrice carrée avec des zéros presque partout sauf sur les r premiers éléments de la diagonale. J'ai donc dit qu'il existe 2 matrices carrés inversibles P et Q telles que A=QJrP. Puis j'ai écrit Jr sous la forme Jr= sigma de 1 à r des EitEi, où (Ei ) est la base canonique de Mn,1(K). A la fin j'ai posé Xi=QEi et Yi=tPEi. Pour finir j'ai montré que les 2 familles étaient libres.
Pour finir cet exercice, je dois montrer que si (X1, ... , Xn) et (Y1, ... , Yn) sont 2 bases de Mn,1(K), alors la famille (XitYj) est une base de Mn(K).
En fait c'est une famille de nxn éléments qui est la dimension de Mn(K).
Il me reste à utiliser le 3è pour montrer que c'est une famille génératrice de Mn(K). Et je pourrai conclure.
Je cherche...
Re: DM sur les matrices de rang r
Bonjour
Même sans les balises tex tu peux écrire Y^t (c'est plus lisible) .
Concernant ta question ma réponse c'est oui c'est un peu cela. a) où X est un vecteur colonne et (a)
a) où X est un vecteur colonne et (a)
une matrice de taille 1 est égal à : a X. Ajouter une ( ) ne change rien (a)X et de toute façon c'est cohérent si on identifie la matrice (a) avec le nombre a qu'elle contient.
pour ta 3 ème question c'est pas plus simple de montrer que c'est une famille libre?
En effet tu prends une combinaison linéaire triviale et tu multiplies par le vecteur Y_1'' tel que je l'ai défini dans la question précédente et le résultat est immédiat.
(puis de même avec i=2,...)
Même sans les balises tex tu peux écrire Y^t (c'est plus lisible) .
Concernant ta question ma réponse c'est oui c'est un peu cela.
 a) où X est un vecteur colonne et (a)
a) où X est un vecteur colonne et (a) une matrice de taille 1 est égal à : a X. Ajouter une ( ) ne change rien (a)X et de toute façon c'est cohérent si on identifie la matrice (a) avec le nombre a qu'elle contient.
pour ta 3 ème question c'est pas plus simple de montrer que c'est une famille libre?
En effet tu prends une combinaison linéaire triviale et tu multiplies par le vecteur Y_1'' tel que je l'ai défini dans la question précédente et le résultat est immédiat.
(puis de même avec i=2,...)
Re: DM sur les matrices de rang r
Pour la directe perso j'aurai procédé comme ceci.
Soit M de rang r alors soit X_1,X_2,..,X_r une base qcq de l'image de M et U un vecteur quelconque.
Alors X_i) où les coefficients c_i(U) dépendent de U mais on vérifie aisément que
où les coefficients c_i(U) dépendent de U mais on vérifie aisément que
c_i(U) dépendent lineairement de U c_i est une forme linéaire) . Il existe donc des vecteurs (colonnes) Y_i,i=1,...,r
tel que c_i(U)=Y_i^t U (identification de tout à l'heure).
On a donc X_i= \sum_{i=1} ^r X_i Y_i^t U)
d'où
reste à montrer l'indépendance des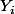
(mais bon pour moi la proposition de la directe et de la réciproque sont étroitement liées car la démo est dans le même esprit)
Soit M de rang r alors soit X_1,X_2,..,X_r une base qcq de l'image de M et U un vecteur quelconque.
Alors
c_i(U) dépendent lineairement de U c_i est une forme linéaire) . Il existe donc des vecteurs (colonnes) Y_i,i=1,...,r
tel que c_i(U)=Y_i^t U (identification de tout à l'heure).
On a donc
d'où
reste à montrer l'indépendance des
(mais bon pour moi la proposition de la directe et de la réciproque sont étroitement liées car la démo est dans le même esprit)
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
