Bonjour à tous,
Voici un problème sur lequel je sèche depuis une semaine.
Soit a<0<b, et soit f continue définie sur [0 ; 1] à valeurs dans [a ; b] telle que l'intégrale de 0 à 1 de f(t) dt vaut 0.
Montrer que l'intégrale de 0 à 1 de f(t)² est inférieure à -ab.
Des idées ?
Merci d'avance.
Majoration d'intégrale
6 messages
- Page 1 sur 1
Re: Majoration d'intégrale
Bonjour
Pour une raison de rédac je remplace à par -a. (a>0,b>0 et f est à valeurs dans [-a,b]).
On pose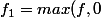) et
et 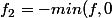.) Ces 2 fonctions vérifient :
Ces 2 fonctions vérifient :
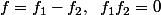
Donc^2 dx=\int_0^1 f_1(x)^2 dx+\int_0^1 f_2(x)^2 dx)
On a aussi et
et 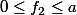
On désigne par la mesure du support de
la mesure du support de  et alors la mesure du support de
et alors la mesure du support de  est majoré par
est majoré par )
On a alors dx \leq b\omega) et
et  dx \leq a(1-\omega))
Donc on reprend les calculs :
^2 dx=\int_0^1 f_1(x)^2 dx+\int_0^1 f_2(x)^2 dx)
 dx +a \int_0^1 f_2(x) dx)
 + ab (\omega)= ab) (comprendre que je viens d'utiliser l'hypothèse qui se
(comprendre que je viens d'utiliser l'hypothèse qui se
traduit par dx =\int_0^1 f_2(x) dx) ) C.Q.F. D
) C.Q.F. D
Pour une raison de rédac je remplace à par -a. (a>0,b>0 et f est à valeurs dans [-a,b]).
On pose
Donc
On a aussi
On désigne par
On a alors
Donc on reprend les calculs :
traduit par
Re: Majoration d'intégrale
Bonjour
J'ai tout de même une remarque. A quoi sert l'hypothèse de continuité?
L'intégrabilité suffit. Mais peut être que l'auteur la question a une autre solution en tête qui lui demande cette
hypothèse en plus.
J'ai tout de même une remarque. A quoi sert l'hypothèse de continuité?
L'intégrabilité suffit. Mais peut être que l'auteur la question a une autre solution en tête qui lui demande cette
hypothèse en plus.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
