Équation Trigonométrique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
ThonySp
- Messages: 4
- Enregistré le: 11 Avr 2019, 12:13
-
 par ThonySp » 11 Avr 2019, 12:23
par ThonySp » 11 Avr 2019, 12:23
Bonjour,
Je suis un peu coincé sur une équation ci-dessous.
.\sin x + 4 - \sqrt{3} = 0)
Je sens qu'il faut utiliser :
- poser

- convertir les
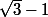
et

par des formes trigonométriques pour faciliter la résolution
Mon raisonnement est juste ?
Merci d'avance !
-
aviateur
 par aviateur » 11 Avr 2019, 12:43
par aviateur » 11 Avr 2019, 12:43
Bonjour
Il ne s'agit pas de raisonnement mais d'une idée. Alors a priori je pense que l'idée n'est pas bonne car comment tu vas faire?
Ce qu'il faut voir c'est que tu as cos^2(x)=1-sin(x)^2. Et tu poses X=sin(x)...
-
ThonySp
- Messages: 4
- Enregistré le: 11 Avr 2019, 12:13
-
 par ThonySp » 11 Avr 2019, 12:53
par ThonySp » 11 Avr 2019, 12:53
Rebonjour,
En attendant, j'ai essayé des solutions et là je tombe sur le principe de
 + \sin^{2}(x) = 1)
. Du coup ta proposition.
Equation résolue par la suite avec
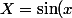)
.
Voici les solutions au cas où :

ou
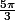

ou
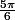
Merci

!
-
aymanemaysae
- Habitué(e)
- Messages: 1265
- Enregistré le: 06 Sep 2013, 14:21
-
 par aymanemaysae » 11 Avr 2019, 13:30
par aymanemaysae » 11 Avr 2019, 13:30
Bonjour;
+2(\sqrt3-1)sin(x)+4-\sqrt3=0)
)+2(\sqrt3-1)sin(x)+4-\sqrt3=0)
+2(\sqrt3-1)sin(x)+4-\sqrt3=0)
+2(\sqrt3-1)sin(x)-\sqrt3=0)
.
Résolvons l'équation :
x-\sqrt3=0)
On a :
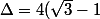^2+16\sqrt3 = 4(3-2\sqrt3+1)+16\sqrt3 = 4(4-2\sqrt3)+16\sqrt3)
=4(1+2\sqrt3+3)=4(1+2\sqrt3+{\sqrt3}^2))
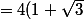^2 = (2(1+\sqrt3))^2=(2+2\sqrt3)^2)
;
donc :
-2-2\sqrt3}{8}=\dfrac{-2\sqrt3+2-2-2\sqrt3}{8}=-\dfrac{4\sqrt3}{8}=-\dfrac{\sqrt3}{2})
;
et
+2+2\sqrt3}{8}=\dfrac{-2\sqrt3+2+2+2\sqrt3}{8}=\dfrac{4}{8}=\dfrac{1}{2})
.
A toi maintenant l'honneur de conclure .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
 !
!