Transitivité

[wilfred1995]

On définit sur la relation définie par:

Montrer que R est une relation d'équivalence et déterminer ses classes d'équivalence

c'est ce que l'exercice dit.

[aviateur]

Heu!! j'ai pas bien compris la définition de R, il manque quelque chose.

[wilfred1995]

j'ai fait une erreur je voulais prendre une partie oubliant que je modifiait plutot

[aviateur]

j'ai fait une erreur je voulais prendre une partie oubliant que je modifiait plutot

Avec ça on n'est pas plus avancé X R y ssi x-y mais quoi?????

C'est simple x R y "si est en relation avec y" ça a du sens, il y a un verbe
x- y "x moins y" il n'y a pas de verbe! Comprenne qui pourra.

[wilfred1995]

On définit sur la relation définie par:
est pair
Montrer que R est une relation d'équivalence et déterminer ses classes d'équivalence

mais il nous avait demande d'enlever, pour finir moi même je ne comprends plus

[aviateur]

Bon enfin! (on ne peut pas deviner)
Maintenant ce n'est pas vraiment difficile. Est-ce que tu peux dire ce que tu as fait?

[wilfred1995]

ok

[wilfred1995]

* Soit
est pair

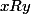
* Soient Supposons montrons que
On a


est pair

* Soient
Supposons que et montrons que xRz
On a (a)+(b) donne z-x=4(k_1+k_2) est pair donc xRz

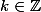
maintenant je ne sais pas si mon est juste

[wilfred1995]

la classe d'equivalence est [x]= les restes de la division de y par 2

[aviateur]

Rebonjour
Alors c'est OK.
Sauf la rédaction. Par exemple pour la réflexivité tu dis
Et bien en soi même, ça veut rien dire.

La réflexivité c'est Ok

Donc une rédaction possible c'est
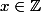
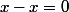
Soit quelconque. On a et 0 est pair. Donc . c.q.f.d.

Le problème de la rédaction c'est pas rien.

[wilfred1995]

merci je m'améliorai au fur et a mesure
ma classe d'équivalence est correct?

[aviateur]

Oui, c'est encore très mal dit.
Il y classe 2 classes d'équivalences. Les nombres pairs et les nombres impairs.
Ou alors la classe des nombres =0 mod(2) et la classe des nombre =1 mod(2)

[wilfred1995]

Ah oui car si x=0 y sera pair sinon impair