Arithmétique dans Z

[Quanto]

soient a,b,c,d € Z* tels que :

pgcd(a:b)=pgcd(c:d)=1

montrer que :
pgcd(ac:bd)= pgcd(a:d) x pgcd(b:c)

[VieuxCrouton]

Par quel entier N peux-tu diviser simultanément ac et bd ?
N ne peux pas diviser simultanément a et b (puisqu'ils sont premiers entre eux)
N ne peux pas diviser simultanément c et d (puisqu'ils sont premiers entre eux)
N ne peut donc diviser simultanément a et d, ainsi que c et b.
Le plus grand diviseur commun de a et d est pgcd(a:d)
Le plus grand diviseur commun de c et b est pgcd(b:c)
La plus grande valeur de N est donc M = pgcd(a:d) x pgcd(b:c)
Et lorsque tu divises ac et bd par M il reste deux entiers premiers entre eux.
Tu les as donc divisé par leur PGCD

[aviateur]

Par quel entier N peux-tu diviser simultanément ac et bd ?
N ne peux pas diviser simultanément a et b (puisqu'ils sont premiers entre eux)
N ne peux pas diviser simultanément c et d (puisqu'ils sont premiers entre eux)
N ne peut donc diviser simultanément a et d, ainsi que c et b.
Le plus grand diviseur commun de a et d est pgcd(a:d)
Le plus grand diviseur commun de c et b est pgcd(b:c)
La plus grande valeur de N est donc M = pgcd(a:d) x pgcd(b:c) (**)
Et lorsque tu divises ac et bd par M il reste deux entiers premiers entre eux.
Tu les as donc divisé par leur PGCD

Bonjour
Je ne suis pas d'accord avec tout cela, ce n'est pas très rigoureux.
rien que les deux premières lignes ça tient pas la route:
"N ne peux pas diviser simultanément a et b (puisqu'ils sont premiers entre eux)"
et N=1?
D'autre part dans la suite il n'y a pas de connexions logique.
En particulier la ligne où j'ai mis (**) c'est la conséquence de quoi???

[VieuxCrouton]

Bonjour.
J'aurais effectivement du préciser au départ que je propose de chercher un entier N supérieur à 1 qui divise simultanément ac et bd. Ensuite j'essaie d'expliquer que N doit être à la fois un diviseur commun à a et d ainsi qu'un diviseur commun à c et b. La plus grande valeur possible de N est donc le produit des PGCD, c'est à dire M = (a^d )* (c^b).

Il me semble que le raisonnement est correct même si la démarche n'est pas rigoureuse. Je veux juste aider, pas résoudre l'exercice. Désolé si je n'y suis pas arrivé.

Je crois que vous devriez être plus tolérant et plus ouvert monsieur l'aviateur.

[Sake]

Bonjour,

Remarque que PGCD(pa+qb,pc+qd) = PGCD(pa+qb,d(pa+qb)-b(pc+qd))

[aviateur]

Je crois que vous devriez être plus tolérant et plus ouvert monsieur l'aviateur.

Bonjour
Je suis tolérant et ouvert. Et je suis aussi un peu mathématicien. Bref on est sur un forum de math et quand une démonstration n'est pas une démonstration et bien il faut le dire.

Il me semble que le raisonnement est correct même si la démarche n'est pas rigoureuse. Je veux juste aider, pas résoudre l'exercice. Désolé si je n'y suis pas arrivé.

Je suis désolé de le répéter le raisonnement n'est pas correct et la démarche n'est pas rigoureuse.
Comme je l'ai dit il y a des affirmations sans justification logique et être ouvert c'est de comprendre cela.
Par contre tu as raison d'essayer d'aider mais il faut s'attendre à accepter d'être critiquer, ou la critique est
comprendre dans le bon sens du terme.

Ici je regarde un film mais dès que j'aurai le temps je ferai la démonstration à moins que quelqu'un ne l'ai fait entre temps.

P.S je n'ai pas réfléchi à la remarque de @shake

[aviateur]

Rebonjour
Il faut démontrer que pgcg(ac,bd)=pgcd(a,d)xpgcd(b,c)
Posons
Ce qui est équivalent à montrer que A divise à la fois ac et bd (1) et que tout diviseur commun de ac et bd divise A (2).
Posons la décomposition en facteur premier de A.
Montrons (1):
Soit fixé. divise A donc il divise pgcd(a,d) ou pgcd(b,c) mais il ne peut diviser les deux à la fois. En effet par exemple s'il divise pgcd(a,d), il divise à la fois a et d mais ne peut diviser ni b, ni c à cause des hypothèses.
Mais alors puisque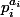 divise A divise, il divise pgcd(a,d) ou pgcd(b,c) mais il ne peut diviser les deux à la fois.
Si par exemple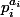 divise pgcd(a,d) il divise a donc ac et il divise b donc bd.
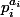divise donc pgcd(ac,bd). J'ai donc montré (1)
Montrons maintenant (2).
Soit B un diviseur commun de ac et bd et un terme quelconque de sa décomposition en facteur premier (i.e q est premier)
q divise ad et supposons que q divise a, il ne peut diviser b (cf hypothèse) donc il divise d. Mais alors il en est de même pour . Donc divise pgcd(a,b) donc A.
Raisonnement analogue si on avait q divise d.
On tire de cela que B divise A. On a montré (2)
Ce qui termine la démo.

[VieuxCrouton]

Et moi je te répète que je n'ai pas cherché à faire une démonstration mais à juste à montrer la voie, à donner une intuition. C'est le plus important pour aider quelqu'un à comprendre. Il ne sert à rien de faire de la cuisine avec des formules si la personne n'a pas compris le fond. Et je répète aussi que mon raisonnement est correct. Si tu ne comprends pas mon raisonnement j'en suis navré, mais ce n'est pas une preuve qu'il est incorrect, sois un peu plus réservé sur ton jugements.

Voici une démonstration qui suit mon raisonnement.(je note x^y le PGCD de x et y)
Posons p = a^d = alors a = p.a' et d= p.d' avec a'^d' = 1
Posons q = b^c = alors b = q.b' et c = q.c' avec b'^c' = 1

Comme les 4 entiers a', b', c', d' sont premiers entre eux, le produit de deux d'entre eux est premier avec le produit des deux autres. Donc a'.b'^c'.d' = 1

On peut écrire a.b = p.q.a'.b' et c.d = p.q.c'.d'
Ce qui montre que (a.b)^(c.d) = p.q = (a^d).(b^c)

[aviateur]

Rebonjour
Je n'ai pas tout lu mais le début maintenant ressemble à quelque chose.
Ce qui n'était pas du tout pas le cas la première fois. C'est tout.
Ensuite je n'ai fait que constater que ce qui était et sans agressivité.
Alors s'il te plait fait de même.

[VieuxCrouton]

Je réponds exactement sur le même ton que toi. Il me semble que je n'ai jamais porté de jugement sur tes messages alors que toi cela fait plusieurs fois que tu te permets de juger mes réponses ou mes questions. Alors je te demande juste une chose : dorénavant ne réponds plus à mes questions si tu ne les comprends pas, et ne juge pas les réponses que je fais aux autres.

[VieuxCrouton]

Évidemment il n'y a pas réciprocité mais dans ta petite cervelle de moineau cela ne te vient pas à l'esprit que je n'écris pas de conneries que mes phrases ont du sens, '' '' ' bref que tu auras du mal à dire que je berdouille comme toi,
Tu porte bien ton surnom et ne t inquiètes pas la prochaine merde que tu ecriras elle ne passera pas car pour moi la priorité c'est les math

Voici ce que tu m'as répondu par message privé ! Tu te prends vraiment pour qui pour porter des jugements pareils et pour t'autoriser un tel langage ?

[aviateur]

en mp pour car je n'ai pas chercher à polémiquer en public comme tu as cherché à le faire et encore ici.
Cela veut dire que d'après toi on ne peut pas relever qu'une démonstration ne va pas (il n'y avait pas de démonstration et même pas d'indication à la démonstration) sans se faire qualifier d'intolérant et de caractère non ouvert. L'intolérance est là.
D'ailleurs je n'ai pas encore relu ta seconde démonstration (qui n'a rien à voir avec ton premier message et là il y a du raisonnement). Mais ne t'inquiètes pas, je vais la lire dès que j'ai le temps et si il y a des fautes, je ne me generai pas de le dire. Evidemment, si elle est correcte et quelque part plus concise que ce que j'ai fait ne t'inquiètes pas je le dirai aussi. D'ailleurs au passage, je ne me prends pas pour plus qu'un autre, ma démonstration peut ne pas être correcte, ou trop concise ou je ne sais pas.

Maintenant la seule prétention que j'ai, c'est de comprendre un peu les math, alors c'est tout à fait normal de corriger quand il le faut.
Mais si tu réfléchis un peu, tu ne peux pas me dire que je n'ai pas à rectifier ou commenter ton message puisque toi tu ne te permets de le faire pour les miens. Et bien ton dictat, c'est n'importe quoi
parce que dans l'ensemble je ne donne pas trop l'occasion de le faire. "Si tu réfléchis un peu" en privé ça fait "petite cervelle de moineau" désolé mais faut pas venir me chercher là où i ne faut pas alors que quand je viens ici c'est défendre les maths et pas autre chose.
Encore une fois ça me gonfle de perdre du temps ici pour des conneries pareilles. Merci de stopper là.

[VieuxCrouton]

Pourquoi t'obstines-tu à me reprocher que ma démonstration n'était pas bonne ? Cela fait 3 fois que je te le dis : je n'ai pas cherché à construire une démonstration. J'ai fini par t'en donner une (et tu constateras probablement qu'elle est correcte quand tu auras pris la peine de l'étudier) mais j'estime que ce n'est pas bien lorsque la question émane, comme c'était visiblement le cas ici, d'un élève qui cherche à résoudre un exercice. Pour aider quelqu'un à résoudre un exercice, la meilleure façon est de le guider en lui faisant remarquer des choses, de susciter une intuition dans son esprit, afin qu'il rédige lui même la démonstration. C'est ce que j'ai voulu faire dans mon premier message. Tu ne t'es même pas donné la peine d'essayer de comprendre quelle est l'idée sous-jacente à la démarche que je propose et tu affirmes encore maintenant que mon raisonnement est incorrect alors que la démonstration que je t'ai donnée s'appuie sur ce raisonnement et arrive au bon résultat.

Remets-toi en question et cesse de m'importuner. C'est tout ce que je demande.

[aviateur]

Ecoute, je vois que tu me réponds encore. Je ne cherche pas du tout à t'importuner. Tu te trompes vraiment.
Pour l'instant admet que je n'ai pas le temps de lire ta démo (la seconde) et je te dirai (à toi mais aussi à la communauté) ce qu'il en est. Un point c'est tout.
Concernant ton premier message je ne pense pas m'être trompé mais on reverra plus tard.
Tu peux dire ce que tu veux sur mon compte en message privé mais ne vient le faire ici en public car tu m'obliges à me justifier à chaque fois malgré tout et franchement j'ai autre chose à faire que d'aller sur ce terrain.
donc pas de problème je reviendrai sur ta démo, je l'ai dit, un point c'est tout.

[VieuxCrouton]

Je suis désolé de te le dire mais tes messages ne contiennent aucun argument qui justifie ton attitude. Tu dis œuvrer pour le bien des mathématiques et du forum, mais j'en doute beaucoup car les vrais défenseurs de ces dignes institutions sont certainement des personnes respectables et respectueuses. De toutes façons, les règles de conduite sur ce forum (ou sur Internet en général) ne viennent pas au-dessus des règles morales et civiques de notre société. Tu penses être détenteur d'un savoir incontestable qui te permet de juger la qualité des réponses et des questions qui circulent sur ce forum et tu le fais en plus dans des termes agressifs et impolis. Tu devrais juste me présenter des excuses et je te promets qu'alors on en restera là.

[aviateur]

Et moi je te répète que je n'ai pas cherché à faire une démonstration mais à juste à montrer la voie, à donner une intuition. C'est le plus important pour aider quelqu'un à comprendre. Il ne sert à rien de faire de la cuisine avec des formules si la personne n'a pas compris le fond. Et je répète aussi que mon raisonnement est correct. Si tu ne comprends pas mon raisonnement j'en suis navré, mais ce n'est pas une preuve qu'il est incorrect,sois un peu plus réservé sur ton jugements.

Voici une démonstration qui suit mon raisonnement.(je note x^y le PGCD de x et y)
Posons p = pgcd(a,d) = alors a = p.a' et d= p.d' avec pgcd(a',d') = 1
Posons q =pgcd( b,c )= alors b = q.b' et c = q.c' avec pgcd(b',c') = 1

Comme les 4 entiers a', b', c', d' sont premiers entre eux, le produit de deux d'entre eux est premier avec le produit des deux autres. Donc pgcd(a'.b',c'.d') = 1

On peut écrire a.b = p.q.a'.b' et c.d = p.q.c'.d'
Ce qui montre que (a.b)^(c.d) = p.q = (a^d).(b^c)

Voici ta deuxième démonstration dont j'avais lu juste le début. Mais rapidement on voit ici qu'elle est complètement fausse (voir la phrase en rouge).
Exemple
a=20; b= 7; c=28; d=5;
Les hypothèses sont vérifiées
p= pgcd(a,d)=5; avec les notations de @vieuxcrouton on a:
a'=a/p= 4 d'=d/p=1
De même
q= pgcd(b,c)=7 et b'=b/q=1; c'=c/q=4
alors il affirme que a',d', b' et c' sont premiers entre eux......(j'en suis pas convaincu du tout )
et que a'.b'^c.'d'=1. or a'b'=4 et c'd'=4
mais pour moi pgcd(a'b',c'd')=4. Ta démonstration est fausse. Il n'y avait rien de bien dans ton premier et ici ta démonstration qui avait l'allure d'un petit quelque chose au début, et bien on voit, qu'il n'y a rien non plus. Et c'est pas en faisant une insulte à mon intelligence, en disant que je ne suis pas capable de comprendre, qu'elle va en devenir meilleure.
Je pense que c'est suffisamment parlant. Que la critique au bon sens du terme doit être acceptée.
Encore même, me serait-je trompé, ça arrive, il suffirait d'argumenter par a+b que tu avais raison.
Alors moi j'arrête là.
Mais je demande aux modérateurs d'être plus prompt (plus rapide) à verrouiller de tels messages.

[VieuxCrouton]

C'est vrai ma démonstration est fausse. J'en suis désolé je croyais sincèrement qu'elle était juste, j'ai probablement sauté une étape ou deux dans le raisonnement. J'aurais du mieux réfléchir.
Pierre