Formule intégrale de Cauchy

[Celmar2Ceaumar]

Bonjour,

je ne comprends pas une subtilité, certainement évidente.

Le théorème de Cauchy nous dit que pour une fonction holomorphe sur un ouvert connexe de C, l'intégrale de cette fonction sur un lacet rectifiable vaut 0.

Alors pourquoi dans la formule intégrale de Cauchy l'expression ne vaut pas 0 elle aussi ?
https://fr.wikipedia.org/wiki/Formule_intégrale_de_Cauchy
En effet quitte à poser f(ξ):=f(ξ)/ξ-z, on a bien là une fonction holomorphe dont l'intégrale sur une courbe fermée simple doit valoir 0...

je vous remercie. Bonne journée.

[aviateur]

Bonjour
Pour la simple raison que la fonction n'est pas holomorphe à l'intérieur du lacet!!

[tournesol]

"Holomorphe sur un ouvert connexe " n'entraine pas la nullité de l'intégrale comme pour la formule intégrale de CY .
c'est "holomorphe sur un ouvert simplement connexe", (ie connexe et sans trou) qui entraîne la nullité de l'intégrale .

[aviateur]

Bonjour
En fait je crois que tu fais une confusion:
Si je prends tout simplement f(z)=1 (qui est bien entendu holomorphe)
La formule intégrale de Cauchy dit que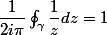 où
est le cercle de centre 0 et de rayon 1 parcouru dans le sens usuel.

Mais f(z)=sin(z) donne
parce que g(z)=sin(z)/z est holomorphe (avec g(0)=1.)

[tournesol]

Je ne fais pas de confusion sur ce sujet .
Soit f holomorphe sur un ouvert simplement connexe et une courbe fermée incluse dans
Alors
La formule intégrale de Cauchy par exemple montre que la nullité de l'intégrale n'est pas assurée si l'ouvert n'est pas simplement connexe car f(z)/z n'est pas nécéssairement holomorphe en 0 .
Il est bien évident que si la fonction f(z)/z est holomorphe au voisinage de 0 , elle n'a pas de résidu en 0 et l'intégrale de la formule de CY sera nulle.

[aviateur]

Bonjour
@tournesol je me doute bien que tu n'as pas fait de confusion. Excuse-moi mais c'est à @cellmar que je répondais.
En fait je voulais compléter ma réponse. Je crois qu'il a confondu intégrer f(z) qui est holomorphe
et f(z)/(z-\xhi) où seulement le numérateur est holomorphe mais z-->f(z)/(z-\xhi) ne l'est pas.