Distribution ??

par **Saadcod** » 30 Mar 2019, 18:54

bonsoir tt le monde
s'il vous plait comment on peut montrer que cette

est une distribution
et merci d'avance

par **mathelot** » 30 Mar 2019, 19:15

bonsoir,
il suffit de montrer que

appartient à

,i.e, que ln() est localement intégrable (au sens de Lebesgue)

or

par **Saadcod** » 30 Mar 2019, 19:25

merci pour votre attention mais je vois qu'il faut appliquer la définition de la distribution on montre que

tend vers

(la continuité)

par **mathelot** » 30 Mar 2019, 19:56

Quelles sont les propriétés des

?

par **Saadcod** » 30 Mar 2019, 20:00

suite des fonctions-test de classe l'infini...

par **aviateur** » 30 Mar 2019, 21:28

Saadcod a écrit:bonsoir tt le monde
s'il vous plait comment on peut montrer que cette
est une distribution
et merci d'avance

Bonjour, d'abord il faut pas confondre "

" et la distribution T. Ensuite ça serait pas idiot d'être plus précis dans la question.
Autrement dit la question correcte c'est: montrer que

définit une distribution (i.e

Maintenant, une des premières propriétés qui découle de la définition c'est que toute fonction

définit une distribution. Normalement c'est la réponse.
Maintenant si tu as une suite

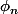
qui converge vers 0 dans

(convergence au sens qui est donné dans ton cours), et bien, en particulier, cela implique qu' il existe un compact

tel que

et

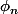
converge uniformément vers 0.
Alors

Ce qui montre que

. C.Q.F.D

par **Saadcod** » 31 Mar 2019, 12:57

Merci beaucoup pour votre aide précieuse, la prochaine fois je vais détailler les choses