Bonjour,
Je vous sollicite car je bloque depuis un certain temps sur les deux dernières questions de l'exercice suivant : http://www.noelshack.com/2019-11-7-1552 ... apture.png
Je vous remercie d'avance pour votre temps !
[Fonctions plusieurs variables] Aide exercice
10 messages
- Page 1 sur 1
Re: [Fonctions plusieurs variables] Aide exercice
4 : x=0, y= -M avec M grand suffit il me semble sans avoir fait le reste
5: j'ai des doutes quand on regarde la partie de la droite y+ax=0 incluse dans A, mais je suis pas pro de ce genre de question.
5: j'ai des doutes quand on regarde la partie de la droite y+ax=0 incluse dans A, mais je suis pas pro de ce genre de question.
Re: [Fonctions plusieurs variables] Aide exercice
Merci pour votre réponse, je bloque toujours sur cette question 
Re: [Fonctions plusieurs variables] Aide exercice
bonsoir,
1) L'intersection est convexe
2) on remplace y = 1-x dans U, on trouve V(x)=U(x,1-x) est un trinôme de la variable x,
qui possède un minimum sur R
4) On fait tendre (0;y) vers l'infini. U(0;y) tend vers plus l'infini quand y tend vers l'infini.
1) L'intersection est convexe
2) on remplace y = 1-x dans U, on trouve V(x)=U(x,1-x) est un trinôme de la variable x,
qui possède un minimum sur R
4) On fait tendre (0;y) vers l'infini. U(0;y) tend vers plus l'infini quand y tend vers l'infini.
Re: [Fonctions plusieurs variables] Aide exercice
Je vous remercie pour votre réponse, auriez-vous une piste pour la question 5 ?
Re: [Fonctions plusieurs variables] Aide exercice
Bonjour
Pour la question 5, quand||\rightarrow \infty) avec
avec \in A) c'est clair que
c'est clair que
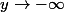 et que
et que 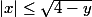 pour
pour 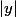 assez grand
assez grand
On a maintenant pour||) assez grand et
assez grand et ) dans A :
dans A :
=-8 a x + a^2 x^2 - 7 y + 2 a x y + y^2\geq -8 a x + a^2 x^2 + 2 a x y + y^2)
\geq -8 |a| |x| + a^2 x^2 -2 |a| |x| |y| + y^2= - 8 |a| |x| +(|a| |x|- |y|)^2)
La contrainte\in A) implique
implique 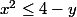 ou encore
ou encore 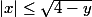
D'où
et alors^2= y^2 +o(y^2)) et
et )
Alors:\geq y^2+o(y^2))
On en déduit que) tend vers
tend vers 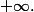
Pour la question 5, quand
On a maintenant pour
La contrainte
D'où
et alors
Alors:
On en déduit que
Modifié en dernier par aviateur le 18 Mar 2019, 09:50, modifié 1 fois.
Re: [Fonctions plusieurs variables] Aide exercice
Bonjour aviateur .
y tend vers mais
mais 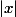 ne tend pas vers
ne tend pas vers  .
.
Ce qui tend vers avec n , c'est le sup de
avec n , c'est le sup de 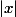 pour
pour |=n) avec
avec ) dans A .
dans A .
y tend vers
Ce qui tend vers
Re: [Fonctions plusieurs variables] Aide exercice
Oui j'ai vu mais et j'ai corrigé, ça n'intervient pas dans la démo.
L'idée c'est que\geq y^2+o(y^2)) et j'ai utilisé uniquement que
et j'ai utilisé uniquement que 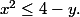
L'idée c'est que
Re: [Fonctions plusieurs variables] Aide exercice
Je vous remercie grandement pour votre aide !
Auriez vous une idée pour cette question :
https://image.noelshack.com/fichiers/2019/12/1/1552904785-screenshot-20190318-111932-drive.jpg
Il s'agit de faire un tracé mais je ne sais pas comment m'y prendre.
Auriez vous une idée pour cette question :
https://image.noelshack.com/fichiers/2019/12/1/1552904785-screenshot-20190318-111932-drive.jpg
Il s'agit de faire un tracé mais je ne sais pas comment m'y prendre.
Re: [Fonctions plusieurs variables] Aide exercice
Bonjour
Rien de bien compliqué excepté un peu de travail:
D'abord tu choisis a et il faut calculer "le fameux" inf.
Vu la question précédente, l'inf est un minimum et il est atteint soit en un point critique ou sur le bord.
Une fois calculé, si on désigne par m sa valeur la courbe à tracer est une conique u(x,y)=m. Donc pas de pb.
Maintenant que tu as un panel de choix de a mais j'ai regardé un peu vite, à chaque fois il me semble que tu as une parabole. Donc quelque soit le choix c'est à peu près le même travail.
Rien de bien compliqué excepté un peu de travail:
D'abord tu choisis a et il faut calculer "le fameux" inf.
Vu la question précédente, l'inf est un minimum et il est atteint soit en un point critique ou sur le bord.
Une fois calculé, si on désigne par m sa valeur la courbe à tracer est une conique u(x,y)=m. Donc pas de pb.
Maintenant que tu as un panel de choix de a mais j'ai regardé un peu vite, à chaque fois il me semble que tu as une parabole. Donc quelque soit le choix c'est à peu près le même travail.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
