équations

[debo8303]

bonjour,j'ai un petit problème je n'arrive pas à résoudre quelques équations pour mon dm de math pouvez vous m'aider svp?

1)9x²-25 / (x+2)(3x+5) = 0
je sais déjà que les valeurs inetrdites sont -2 et -5 mais après j'suis bloqué

2)2x-3 / x+1 = 2x-3 / 2-x
je sais pas comment faire pour que les 2 soit au même dénominateur parce que la 1ère il faut que je multiplie par x-1 et la 2eme 2+x mais seulement les dénominateurs seront pas égaux

3)2 / (x-2)² - 2/x-2 = 0

[Zebulon]

Bonsoir,

1)9x²-25 / (x+2)(3x+5) = 0
je sais déjà que les valeurs inetrdites sont -2 et -5

les valeurs interdites sont les solutions de x+2=0 et les solutions de 3x+5=0.
OK
et

[debo8303]

merci
mais après pour le 9x² -25 ? c'est 9x²=25
x=25/9
?

[Zebulon]

mais après pour le 9x² -25 ?

Il faut reconnaître une identité remarquable...

[yggdrasiil]

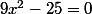
Non, il faut trouver les solutions pour . Donc soit tu utilises la formule de résolution des équations du deuxième degré, soit tu résouds directement vu que ton équation est plutôt simple.





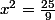
Ce qui donne au signe près.

[Zebulon]

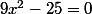
Non, il faut trouver les solutions pour . Donc soit tu utilises la formule de résolution des équations du deuxième degré, soit tu résouds directement vu que ton équation est plutôt simple.

Et remarquer que c'est une identité remarquable ?

[debo8303]

merci beaucoup à tous les deux

[Zebulon]

a²-b², ça ne vous rappelle rien ?

[yggdrasiil]

C'est à ceci que je répondais non :

merci
mais après pour le ? c'est

?

Pas à toi :++:

[yggdrasiil]

a²-b², ça ne vous rappelle rien ?

Si, même pas mal de choses en fait. Quelque chose comme ? :id:

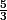
Effectivement, là on voir sur-le-champ que les solutions sont de au signe près.

[debo8303]

donc sa fera si j'ai bien compris :
9x²-25=0 x+2=0 3x+5=0
9x²=25 x=-2 3x=-5
x=25/9 x=-5/3
x=V25/9

la solution de x+2 est valeur interdite don les solutions sont -5/3 et V25/9

c'est ça?

[Zebulon]

D'une manière générale, .
Donc ici,