Opérateur non borné
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Bigorneau
- Membre Naturel
- Messages: 44
- Enregistré le: 23 Sep 2017, 19:04
- Localisation: France
-
 par Bigorneau » 12 Mar 2019, 15:05
par Bigorneau » 12 Mar 2019, 15:05
Bonjour à tous, voici une question qui me tracasse. Soit un opérateur linéaire
 \longrightarrow C^\infty_0(\R^3))
défini pour
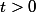
. On veut montrer que
 = \partial_t \left( \frac{1}{t} \int_{\partial B_1(0)} f(x+ty) \, dS(y) \right) = \partial_t (\delta(t - |x-y|), f))
n'est pas un opérateur borné sur
)
pour
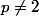
. Après calcul j'obtiens une inégalité de la forme :
 \|_{p} \geq \frac{1}{t} \left| \| \int_{B_1(0)} \Delta f(x+ty) \, dy \|_{p} - \frac{1}{t} \| \int_{\partial B_1(0)} f(x+ty) \, d S(y) \|_{p} \right|)
.
Sauf qu'à partir de là je ne parviens pas à trouver une suite de fonction qui pourrait violer la continuité.
Toute proposition est la bienvenue

(je peux donner plus de contexte si nécessaire).
Modifié en dernier par
Bigorneau le 12 Mar 2019, 18:56, modifié 1 fois.
-
aviateur
 par aviateur » 12 Mar 2019, 15:54
par aviateur » 12 Mar 2019, 15:54
Bonjour
L'écriture est perturbante :
=....)
c'est plutôt
(x))
je pense.
Ensuite on devine que

représente la mesure de Dirac mais
,f))
ça veut dire quoi?
C'est peut être une notation particulière donnée dans l'exercice mais il faut le préciser.
B_1(0) c'est bien la boule unité centré en 0?
De toute façon dans l'inégalité que tu dis avoir démontré, on ne voit pas ce que c'est x.

-
Bigorneau
- Membre Naturel
- Messages: 44
- Enregistré le: 23 Sep 2017, 19:04
- Localisation: France
-
 par Bigorneau » 12 Mar 2019, 16:15
par Bigorneau » 12 Mar 2019, 16:15
Oui en effet on regarde
)
comme une fonction de
)
et on s'intéresse à la norme
 \|_p)
. Aussi
)
est bien la boule.
Au sujet de la distribution de dirac, c'était juste pour l'écrire sous forme d'une distribution,
)
c'est la distribution sur la surface
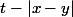
. J'aurais dû l'écrire
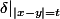
, mais j'avoue que je ne me suis pas servi de la distribution de dirac in fine. J'ai simplement dérivé et utilisé l'inégalité triangulaire.
-
aviateur
 par aviateur » 12 Mar 2019, 16:22
par aviateur » 12 Mar 2019, 16:22
Ok, J'ai encore quelque questions:
t est fixé positif? Par exemple on pourrait commencer par démontrer avec t=1?
Et puis l'inégalité, admettons qu'elle soit vraie. Je ne vois pas pourquoi l'avoir démontrée, quel est le lien avec le fait que A_t ne serait pas bornée?
-
Bigorneau
- Membre Naturel
- Messages: 44
- Enregistré le: 23 Sep 2017, 19:04
- Localisation: France
-
 par Bigorneau » 12 Mar 2019, 16:34
par Bigorneau » 12 Mar 2019, 16:34
Oui

est fixé. Ben je pensais trouver une séquence de fonctions qui converge dans
)
mais avec
\|_p \rightarrow +\infty)
. Sinon, il faudrait alors juste violer la continuité.
Sans l'inégalité on trouve (à moins que je me sois trompé)
(x) = \frac{1}{t}\left( \int_{B_1(0)}\Delta f(x+ty)\, dy - \frac{1}{t}\int_{\partial B_1(0)} f(x+ty)\, dS(y)\right))
Modifié en dernier par
Bigorneau le 12 Mar 2019, 19:16, modifié 1 fois.
-
aviateur
 par aviateur » 12 Mar 2019, 17:14
par aviateur » 12 Mar 2019, 17:14
Bonjour
Une idée peut être à exploiter:
Si tu considères une fonction
,)
paire à support compact. Par exemple [-1,1].
On considère alors la fonction radiale f(x)=
.)
On définit alors les fonctions

définies par
=\omega_n f(nx))
où les
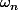
sont choisis de sorte que
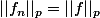
Il serait bien alors de regarder si les normes
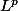
des fonctions
)
explosent.
En particulier, je me demande si c'est le cas à cause du comportement au voisinage 0 des fonctions
)
-
Bigorneau
- Membre Naturel
- Messages: 44
- Enregistré le: 23 Sep 2017, 19:04
- Localisation: France
-
 par Bigorneau » 12 Mar 2019, 18:23
par Bigorneau » 12 Mar 2019, 18:23
Merci pour les commentaires

.
J'ai déjà regardé un peu ce type de fonctions à vrai dire. Par
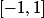
j'imagine que vous vouliez dire
)
(3 dimension spatiale). On a
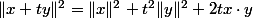
En dérivant :
(x) = \frac{\omega_n}{t} \left( \int_{\partial B_1(0)} \phi'(n \|x+ty\|) \frac{n (x\cdot y + t)}{\|x+ty\|} \, dS(y) - \frac{1}{t} \int_{\partial B_1(0)} \phi(n \|x+ty\|) \, dS(y) \right))
Le fait que

a support compact dans la boule unitaire, nous donne
} \phi'(n \|x+ty\|) \frac{n (x\cdot y + t \| y \|^2)}{\|x+ty\|} \, dS(y) - \frac{1}{t} \int_{\partial B_1(0)} \phi(n \|x+ty\|) \, dS(y) \right|^p \, dx\\<br />= \int_{|x + ty\| \leq 1/n} \left| \int_{\partial B_1(0)} \phi'(n \|x+ty\|) \frac{n (x\cdot y + t )}{\|x+ty\|} \, dS(y) - \frac{1}{t} \int_{\partial B_1(0)} \phi(n \|x+ty\|) \, dS(y) \right|^p \, dx)
Je ne sais pas trop quoi en conclure. Sinon peut-être en regardant les choses sans se plonger dans trop de calculs
(x) = \partial_t \left( \frac{\omega_n}{t} \int_{\partial B_t(x)} \phi(n \| y \|) \, dS(y) \right))
D'où
 \|_p^p = \int_{\R^3} \left| \partial_t \left( \frac{\omega_n}{t} \int_{\partial B_t(x)} \phi(n \| y \|) \, dS(y) \right) \right|^p \, dx<br />= \int_{B_{(1+t)/n}(0)} \left| \partial_t \left( \frac{\omega_n}{t} \int_{\partial B_t(x)} \phi(n \| y \|) \, dS(y) \right) \right|^p \, dx)
Là encore je ne vois pas bien comment finir. D'autant que cela ne nous donne pas d'intuition sur la spécificité du cas
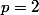
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités