Angles icrits

[Nessyterence]

Bonsoir pouvez vous m'aider à traiter cet exercice je suis bloquée.
Soit ABCD un rectangle tels que BD=2AB et (C) le cercle circonscrit à ABCD. Les tangentes en A et D au cercle (C) ont pour point d'intersection M et coupent la droite (BC) respectivement en Net P. Démontrer que le triangle MNP est équilatéral.

[aviateur]

Bjr,
L'exercice est très simple , je vais pas tout rédiger. Grosso modo
En faisant une figure on peut constater par exemple que
l'angle ABD= 30 degré car son sinus=1/2. Mais on peut faire de même l'angle ACB (que l'on retrouve aussi égal à 30degré gra^ce au th de l'angle inscrit mais qui n'est pas d'une grande utlité dans cet exo!)
Marquer les angles droit comme par exemple (BD) orthogonal à (AP) (tangente en D). Alors de proche en proche on trouve que l'angle en P=60 degrés et par symétrie on trouvera que l'angle en N= 60 degrés. cqfd

[Black Jack]

Salut,

Je présume, ne pas avoir le même dessin que Aviateur ...



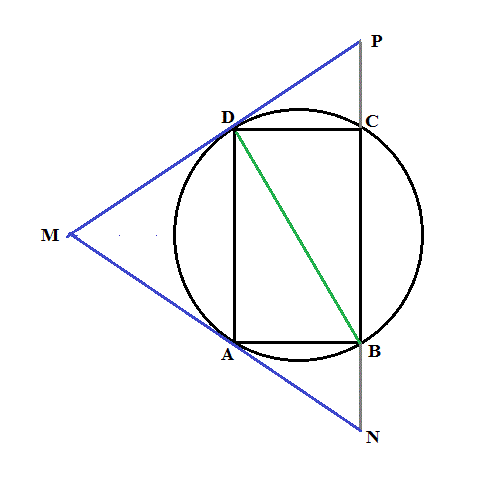
AB = BD.cos(ABD)
cos(ABD) = AB/BD = 1/2
--> Angle(ABD) = 60°

angle(ABD) = angle(BDC) (alterne-interne)
--> Angle(BDC) = 60°

BD passe par le centre du cercle (puisque les diagonale de ABCD se coupent en leurs milieux et donc ...)

MP et BD sont donc perpendiculaires (une tangente à 1 cercle est perpendiculaire au rayon (ou diamètre) du cercle passant par le point de tangence)
--> angle(BDP) = 90°

angle(BDP) = angle(BDC) + angle(CDP) (voir sur dessin)
90° = 60° + angle(CDP)
angle(CDP) = 30°

La somme des angles intérieurs d'un triangle = 180°, et donc, dans le triangle DCP :
angle(CDP) + angle(DCP) + angle(DPC) = 180°
30° + 90° + angle(DPC) = 180°
angle(DPC) = 60°

De manière analogue (en utilisant le fait que BD = AC, puisque les diagonales d'un rectangle se coupent en leurs milieux), on démontre que :
angle(BNA) = 60°

Les angles qu triangles MNP sont donc égaux à 60°, c'est un triangle équilatéral.

[aviateur]

si c'est la même figure, seuls les noms des points ont été échangés

[Black Jack]

Bonjour aviateur,

Je me suis fié à ce qui est souvent admis pour repérer les sommets d'un polygone, soit :

Nommer les sommets en tournant (dans un sens ou dans l'autre) autour de la figure dans l'ordre où ils sont donnés ?

De sorte que pour un rectangle ABCD, on ait : vect(AB) = vect(DC) et pas vect(AB) = vect(CD)

Le polygone sera direct si l'ordre dans lequel les sommets sont cités est le sens contraire des aiguilles d'une montre.

Le polygone sera indirect si l'ordre dans lequel les sommets sont cités est le sens des aiguilles d'une montre.

Ici, que le rectangle soit "direct" ou "indirect" ne change rien dans la démo.
Dans les 2 cas, on a : angle(ABD) = 60°

Je ne comprends pas vraiment comment tu as repéré la figure (emplacement des lettres A,B,C,D,M,N,P) pour avoir angle(ABD) = 30°

[aviateur]

Bonjour black jack
Je viens de vérifier on a la même figure.
J'ai fait une erreur de copie, il ne s'agit pas de l'angle ABD dont je voulais parler mais de l'angle ADB .
dc pas de problème.
En effet on peut prendre l'angle ABD mais il faut prendre son cosinus.
De toute façon c'est équivalent.

[Black Jack]

OK