Bonjour,
Je rencontre de la difficulté sur l’exercice suivant :
Donner la nature de la serie de termes general Un = 1/(n*ln(n)).
Ma réponse :
Je pose : n^a * Un = n^(a-1) / ln(n)
Je sais que la serie converge ssi Un —> 0, donc ssi a<1.
Or d’apres le critère de Riemann la serie de termes general 1/(n^a) converge ssi a > 1.
Donc, par comparaison la serie de termes general Un diverge.
Est ce ma démarche fonctionne ?
Merci pour votre temps d’avance !
Serie numerique
8 messages
- Page 1 sur 1
Re: Serie numerique
Non ton raisonnement ne marche pas car la comparaison n'est pas dans le bon sens, i,e
)< 1/ n, \forall n>1.)
Re: Serie numerique
C’etait mon idée de départ, mais je ne savais comment montrer que l’integrale de x—>1/(xln(x)) était inférieur a la serie de termes general Un
Re: Serie numerique
Rebonjour
La comparaison avec l'intégrale proposée ci-dessus te montre en posant f(x)=ln(ln(x)):
-f(n)<\dfrac{1}{n ln(n)}=u_n) pour tout
pour tout  . (ou ce qui revient au même les accroissements finis)
. (ou ce qui revient au même les accroissements finis)
On a donc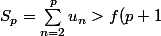-f(2).) (règle des dominos "ça se dit"?)
(règle des dominos "ça se dit"?)
Ce qui montre que les somme partielles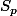 cv vers
cv vers 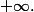
La série est divergente
La comparaison avec l'intégrale proposée ci-dessus te montre en posant f(x)=ln(ln(x)):
On a donc
Ce qui montre que les somme partielles
La série est divergente
Re: Serie numerique
Ah oui d’accord ! J’avais pas pensé à utiliser le th. des accroissements finis..
Merci beaucoup
Bonne soirée
Merci beaucoup
Bonne soirée
Re: Serie numerique
C'est une série dite de Bertrand.
Le critère "grossier" de Riemann ne s'applique pas, le ln(n) passe à travers les mailles du filet de taille n^a...
Il faut donc reprendre le raisonnement utilisé (comparaison série intégrale) pour Riemann, mais avec la fonction proposée par aviateur et mathelot.
Le même raisonnement donnerait la nature de la série de terme général n^a ln(n)^b pour tous a et b réels.
Le critère "grossier" de Riemann ne s'applique pas, le ln(n) passe à travers les mailles du filet de taille n^a...
Il faut donc reprendre le raisonnement utilisé (comparaison série intégrale) pour Riemann, mais avec la fonction proposée par aviateur et mathelot.
Le même raisonnement donnerait la nature de la série de terme général n^a ln(n)^b pour tous a et b réels.
Re: Serie numerique
aviateur a écrit: (règle des dominos "ça se dit"?)
on parle de somme télescopique ^^
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 13 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
