Bonsoir , pouvez-vous m’aider à repondre à cette question et merci d’avance !
Déterminer les reels a,b et c pour que
1/x(x^2 -1)= a/x +b/(x-1) +c/(x+1)
Nombre reels
9 messages
- Page 1 sur 1
Re: Nombre reels
Un premier moyen, mais pas le plus simple, auquel tout le monde peut
penser, c' est de réduire au même dénominateur a/x+b/(x-1)+c/(x+1) et de dire que les numérateurs qui sont des polynômes sont égaux.
Cela te fera 3 équations à trois inconnues à résoudre. Tu peux vérifier ça marche mais c'est pas trop marrant.
Ce qui est mieux , par exemple pour trouver a, c'est de multiplier chaque membre par x:
ce qui donne 1/(x^2-1)=a + b x/(x-1)+cx/(x+1) et de dire que si les deux expressions sont égales, elles restent égales à la limite quand x-> 0 ce qui donne -1 =a . (c'est que j'ai fait de tête pour avoir a)
Pour b on fait pareil on multiplie par x-1 et on fait tendre x vers 1.
c idem.
Il y d'autres astuces (que j'ai utlisé pour répondre + rapidement), par exemple la fonction est impaire donc tu dois avoir b=-c (ça évite de calculer c)
Encore une astuce, tu multiplies tout par x^3 et on fait tendre x vers + l'infini :
A gauche ça tend vers une limite finie donc à droite ça doit tendre vers une limite finie. Mais ce n'est possible que si a+b+c=0.
penser, c' est de réduire au même dénominateur a/x+b/(x-1)+c/(x+1) et de dire que les numérateurs qui sont des polynômes sont égaux.
Cela te fera 3 équations à trois inconnues à résoudre. Tu peux vérifier ça marche mais c'est pas trop marrant.
Ce qui est mieux , par exemple pour trouver a, c'est de multiplier chaque membre par x:
ce qui donne 1/(x^2-1)=a + b x/(x-1)+cx/(x+1) et de dire que si les deux expressions sont égales, elles restent égales à la limite quand x-> 0 ce qui donne -1 =a . (c'est que j'ai fait de tête pour avoir a)
Pour b on fait pareil on multiplie par x-1 et on fait tendre x vers 1.
c idem.
Il y d'autres astuces (que j'ai utlisé pour répondre + rapidement), par exemple la fonction est impaire donc tu dois avoir b=-c (ça évite de calculer c)
Encore une astuce, tu multiplies tout par x^3 et on fait tendre x vers + l'infini :
A gauche ça tend vers une limite finie donc à droite ça doit tendre vers une limite finie. Mais ce n'est possible que si a+b+c=0.
Re: Nombre reels
D’accord merci beaucoup!
Une question !pour la première methode , je l’ai deja essayé sauf que l’expression au numérateur est difficile à resoudre
Y-a-t il une methode?? (Ou c’est impossible de la trouver)
Merci encore !
Une question !pour la première methode , je l’ai deja essayé sauf que l’expression au numérateur est difficile à resoudre
Y-a-t il une methode?? (Ou c’est impossible de la trouver)
Merci encore !
Re: Nombre reels
Normalement tu as dû trouver
x^2 + (b-c) x -a}{x(x^2-1)} = \dfrac{ 1}{x(x^2-1)} \forall x.)
Doncx^2 + (b-c) x -a =1, \forall x.)
donc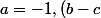=0,) et
et 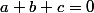
c'est vraiment facile à finir
Donc
donc
c'est vraiment facile à finir
Modifié en dernier par aviateur le 06 Mar 2019, 20:00, modifié 1 fois.
Re: Nombre reels
Salut,
Il faudrait commencer par apprendre l'utilisation correcte des parenthèses et les priorités des opérations mathématiques.
Il y a quelques décennies, c'était le carton rouge immédiat.
1/x(x^2 -1) est équivalent à)
Si tu veux ceci :}) , alors, il FAUT écrire : 1/(x.(x^2-1))
, alors, il FAUT écrire : 1/(x.(x^2-1))
... Ce n'est pas une "petite" erreur.

Il faudrait commencer par apprendre l'utilisation correcte des parenthèses et les priorités des opérations mathématiques.
Il y a quelques décennies, c'était le carton rouge immédiat.
1/x(x^2 -1) est équivalent à
Si tu veux ceci :
... Ce n'est pas une "petite" erreur.
Re: Nombre reels
Il faudrait qu'on lance une demande ,sur la Toile ,en direction des profs de maths francophones , car les problèmes de mauvaises parenthèses (ou d'absence de parenthèses) sont généralisés et pas du tout assimilés.
Re: Nombre reels
mathelot a écrit:Il faudrait qu'on lance une demande ,sur la Toile ,en direction des profs de maths francophones , car les problèmes de mauvaises parenthèses (ou d'absence de parenthèses) sont généralisés et pas du tout assimilés.
A force d'être sur le forum je finirai par m'y habituer malgré moi?
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
