Bonjour,
Est-ce un exercice en particulier ou bien tous ? quels sont vos raisonnements ?
Exercice Urgent SVP
9 messages
- Page 1 sur 1
Re: Exercice Urgent SVP
par Pisigma » 05 Mar 2019, 14:48
Bonjour,
Quel exercice votre fille a-t-elle commencé?
Quelles infos complémentaires a-t-elle ?
Ou bloque-t-elle?
En quelle année est-elle?
sans ces infos, je crains que personne ne puisse vous aider
Quel exercice votre fille a-t-elle commencé?
Quelles infos complémentaires a-t-elle ?
Ou bloque-t-elle?
En quelle année est-elle?
sans ces infos, je crains que personne ne puisse vous aider
Re: Exercice Urgent SVP
par aymanemaysae » 06 Mar 2019, 10:32
Bonjour;
Exercice n° 1 .
Les racines cinquièmes de
sont :
;
donc :
(z-e^{i\dfrac{2\pi}{5}})(z-e^{-i\dfrac{2\pi}{5}})(z-e^{i\dfrac{4\pi}{5}})(z-e^{-i\dfrac{4\pi}{5}}))
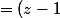(z^2-(e^{i\dfrac{2\pi}{5}}+e^{-i\dfrac{2\pi}{5}})z+1)(z^2-(e^{i\dfrac{4\pi}{5}}+e^{-i\dfrac{4\pi}{5}})z+1))
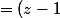(z^2-2zcos(\dfrac{2\pi}{5})+1)+(z^2-2zcos(\dfrac{4\pi}{5})+1)+1))
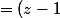(z^4-2(cos(\dfrac{2\pi}{5})+cos(\dfrac{4\pi}{5}))z^3)+2(1+2cos(\dfrac{2\pi}{5})cos(\dfrac{4\pi}{5}))z^2 -2(cos(\dfrac{2\pi}{5})+cos(\dfrac{4\pi}{5}))z+1)
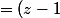(z^4+z^3+z^2+1))
Ceci est vrai pour tout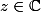
, donc on a par correspondance :
+cos(\dfrac{4\pi}{5})) = 1 \Rightarrow cos(\dfrac{2\pi}{5})+cos(\dfrac{4\pi}{5})=-\dfrac{1}{2})
+2cos^2(\dfrac{2\pi}{5})-1=-\dfrac{1}{2})
+2cos(\dfrac{2\pi}{5})-2=-1\Rightarrow 4cos^2(\dfrac{2\pi}{5})+2cos(\dfrac{2\pi}{5})-1=0)
)^2+(2cos(\dfrac{2\pi}{5}))-1=0)
donc
est solution de l'équation en 
suivante :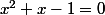 
.
Cette équation a deux solutions :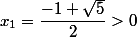
et 
comme>0)
donc  = \dfrac{-1+\sqrt5}{2})
donc  = \dfrac{-1+\sqrt5}{4})
.
On a :=2cos^2(\dfrac{\pi}{5})-1\Rightarrow 2cos^2(\dfrac{\pi}{5})=1+cos(\dfrac{2\pi}{5})=1+ \dfrac{-1+\sqrt5}{4}= \dfrac{3+\sqrt5}{4})
=\dfrac{3+\sqrt5}{8})
.
On a :^2}{16}=(\dfrac{1+\sqrt 5}{4})^2)
,
donc : = (\dfrac{1+\sqrt 5}{4})^2 \Rightarrow cos(\dfrac{\pi}{5}) = \dfrac{1+\sqrt 5}{4})
car on a >0)
.
On a :=cos(\dfrac{2\pi}{10})=cos^2(\dfrac{\pi}{10})-sin^2(\dfrac{\pi}{10})=1-2sin^2(\dfrac{\pi}{10}))
=1-cos(\dfrac{\pi}{5})=1-\dfrac{1+\sqrt 5}{4}=\dfrac{3-\sqrt 5}{4}\Rightarrow sin^2(\dfrac{\pi}{10})=\dfrac{3-\sqrt 5}{8})
+sin^2(\dfrac{\pi}{10})=\dfrac{3+\sqrt 5}{8}+\dfrac{3-\sqrt 5}{8}=\dfrac{6}{8}=\dfrac{3}{4})
.
Exercice n° 1 .
Les racines cinquièmes de
donc :
Ceci est vrai pour tout
donc
Cette équation a deux solutions :
comme
On a :
On a :
donc :
On a :
Re: Exercice Urgent SVP
par aymanemaysae » 06 Mar 2019, 12:34
Bonjour;
Exercice n° 2 .
^2}=\underset{u\rightarrow 2}{lim}\dfrac{16\sqrt{u^2-\sqrt u}-3\sqrt2u^2-4\sqrt2}{(u^2-4)^2})
-4\sqrt2}{v^2(v^2+4)^2})
On a :))
)
;
donc :-4\sqrt2}{v^2(v^2+4)^2})
-4\sqrt2}{v^2(v^2+4)^2})
v^2}{v^2(v^2+4)^2}= \underset{v\rightarrow 0}{lim}\dfrac{-\dfrac{\sqrt2}{2}-3\sqrt2}{(v^2+4)^2}=\underset{v\rightarrow 0}{lim}\dfrac{-\dfrac{7\sqrt2}{2}}{(v^2+4)^2}=-\dfrac{7\sqrt2}{32})
.
Exercice n° 2 .
On a :
donc :
Re: Exercice Urgent SVP
par aymanemaysae » 06 Mar 2019, 12:36
De rien . J'espère que ta petite fille est un peu éclairée maintenant : les réponses à ces questions ne sont pas directes . Je lui souhaite Bon Courage .
Re: Exercice Urgent SVP
par mathelot » 06 Mar 2019, 14:28
pourquoi la jeune fille ne pose-t-elle pas les questions elle-même ? il faut connaitre le programme de L1 pour comprendre la réponse de aymanemaysae
Re: Exercice Urgent SVP
par aymanemaysae » 06 Mar 2019, 15:10
Exercice n° 5 .
On a :)^4 = 1 + 4 i\ tan(a) - 6\ tan^2(a) - 4\ tan^3(a) + tan^4(a))
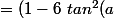 + tan^4(a)) + 4i\ (tan(a)-tan^3(a)))
.
On a aussi :)^4 = \left (\dfrac{cos(a)-i\ sin(a)}{cos(a)}\right)^4=\dfrac{e^{4ia}}{cos^4(a)})
+i\ sin(4a)}{cos^4(a)})
;
donc :}{cos^4(a)} = (1 - 6\ tan^2(a) + tan^4(a)) \ \dfrac{sin(4a)}{cos^4(a)} = 4\ (tan(a)-tan^3(a)))
et = 4\dfrac{tan(a)-tan^3(a)}{1 - 6\ tan^2(a) + tan^4(a)}=\dfrac{120}{119})
.
On a :=\dfrac{tan(4a)-tan(b)}{1+tan(a)tan(b)}=1)
;
donc on a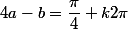
avec 
appartenant à un ensemble de valeurs à définir .
On a :
; donc : 
et
; donc : 
;
donc :
;
donc :
donc :
donc :
donc :
donc :
On a :
On a aussi :
donc :
et
On a :
donc on a
On a :
et
donc :
donc :
donc :
donc :
donc :
donc :
Modifié en dernier par aymanemaysae le 06 Mar 2019, 15:40, modifié 1 fois.
Re: Exercice Urgent SVP
par mathelot » 06 Mar 2019, 15:23
bonjour,
exercice 3: sur quel ensemble de points du plan s'annule la valeur absolue ?
quel est l'ensemble des points tels que
?
quel est l'ensemble des points tels que
?
exercice 3: sur quel ensemble de points du plan s'annule la valeur absolue ?
quel est l'ensemble des points tels que
quel est l'ensemble des points tels que
Re: Exercice Urgent SVP
par Pisigma » 06 Mar 2019, 16:04
Exercice 1
une autre approche
après avoir calculé=16 cos^5(x)-20cos^3(x)+5 cos(x))
on introduit)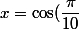
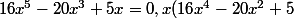=0)
la parenthèse donne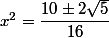
soit
=\dfrac{10+2\sqrt{5}}{16}~~, cos(\dfrac{\pi}{10})=\dfrac{\sqrt{10+2\sqrt{5}}}{4})
=2 cos^2(\dfrac{\pi}{10})-1)
=1- cos^2(\dfrac{\pi}{10}))
une autre approche
après avoir calculé
on introduit
la parenthèse donne
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :