Matrice inversible ???

par **tonythx** » 14 Nov 2006, 20:34

soit A une matrice symétrique nxn définie positive, B une matrice pxn de rang p. Montrer que la matrice

est inversible.
Merci par avance de votre attention!
Tonythx

par **tize** » 14 Nov 2006, 20:53

[EDIT] je retire ce que j'ai dit, ça m'apprendra à parler trop vite...

par **Vir** » 14 Nov 2006, 21:37

En montrant que le determinant est différent de 0 non ?

par **abcd22** » 14 Nov 2006, 21:53

Bonsoir,
On peut essayer de montrer que le noyau de cette matrice est nul : on prend X un vecteur colonne à n lignes, Y un vecteur colonne à p lignes tel que

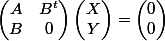
. Ca signifie que

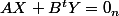
et

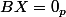
(où l'indice n signifie que c'est un vecteur colonne à n lignes, pareil pour p). On peut multiplier la première égalité par

, la seconde par

...

par **tonythx** » 14 Nov 2006, 22:05

merci en tout cas la dernière proposition est intéressante, je pense m'en sortir
Merci encore

Matrice inversible ???

matrice inversible ???

Qui est en ligne