Numération - question récurrence

[rcompany]

Exercice:



Je reformule la proposition pour faciliter la notation:



Montrons l'existence:





Et ensuite:



Question: peut-on parler de "récurrence", i.e. que l'existence est vraie pour tout n de puisqu'à partir de 1 et 2 et des suites on couvre l'ensemble de ?

On peut résoudre cet exercice en particulier avec une récurrence traditionelle:

L'existence est vraie pour n=1.

Supposons-la vraie pour n quelconque de

• 
  
  
• 
  
  
  
  

[chan79]

salut
Peux-tu préciser l'unicité ?

[aviateur]

Question: peut-on parler de "récurrence", i.e. que l'existence est vraie pour tout n de puisqu'à partir de 1 et 2 et des suites on couvre l'ensemble de ?

Bonjour
Je viens seulement de comprendre où tu voulais en venir.

J'y répondrai (si possible) plus précisément plus tard car ici j'ai pas trop le temps.
Ceci étant d'un point de vue pragmatique, je vois pas trop l'intérêt car justement tu donnes une démo + simple juste après. Mais du point de vue mathématique c'est pas idiot du tout.

[aviateur]

Rebonjour
La réponse à ta question est oui. C'est bien connu qu'il y a divers types de récurrence, mais à ma connaissance celle-ci ne fait pas partie de la panoplie de ce qui est utilisé dans la pratique.
Alors je pense que si (dans un cas exceptionnel) on est amené à l'utiliser, il faut montrer que c'est bien une récurrence.
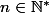
Pour être plus précis, tu as une proposition P(n) qui dépend de et tu veux montrer que P(n) est vraie pour tout
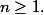
Ensuite tu as montré que P(1) est vraie (P(2) aussi mais c'est inutile) et que si P(n) est vraie alors P(2n+1) et P(2n+2) est vraie. Ta question en fait c'est "est-ce que cela montre que P(n) est vraie quelque soit ?
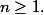
Pour se convaincre que la réponse est oui, il suffit de faire un raisonnement par l'absurde.
En effet, supposons que pour un entier n, P(n) soit faux.
Si n est pair alors d'après ta démo, P(n/2) est faux.
De même si n est impair, P((n-1)/2 ) serait faux.
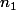
Dans tous les 2 cas cela implique qu'il y a un entier plus que petit que n strictement pour lequel la proposition est fausse. .... on devine la suite c'est à dire que l'on va aboutir à P(1) est faux. D'où la contradiction.

[rcompany]

OK merci, c`est compris

[rcompany]

salut
Peux-tu préciser l'unicité ?

on ne peut pas avoir

[rcompany]

salut
Peux-tu préciser l'unicité ?

Démonstration de l'unicité pour ceux que la résolution de cet exercice en particulier intéresse:

Supposons que l'on ait pour :

• 
• 
  

[aviateur]

Bonjour
Tout ceci étant dit, est ce qu'il faut faire tout ça pour faire l'exercice? Je ne pense pas car l'écriture unique de n
proposée par l'exo . est une conséquence directe de l'écriture unique de n dans la base 2.