Bonjour,
Je voudrais calculer la primitive de
f(x)= x^4 / (1+x)(1+x^2)
mon idée est de la décomposer comme suit
f(x)= A/(1+x)+B/(1+x^2)
mais je n'arrive pas à trouver les formes convenables de A et B ...
Merci.
Calcul de primitives
9 messages
- Page 1 sur 1
Re: calcul de primitives
une façon de faire
tu as du degré 4 en haut, 3 en bas, on peut déjà sortir un polynôme de degré 1 de la fraction
f(x)= x^4 / (1+x)(1+x^2)
f(x)= ax+b +c /(1+x)+(dx+e)/(1+x^2)
a=1 en comparant les termes de degré le plus haut
x^4 / (1+x)(1+x^2) = x(x^3+x²+x+1) / (1+x)(1+x^2) - x(x²+x+1) / (1+x)(1+x^2)
= x - x(x²+x+1) / (1+x)(1+x^2)
= x - ( x(x²+x+1)+1-1) / (1+x)(1+x^2)
= x-1+1/ (1+x)(1+x^2)
il reste à décomposer 1/ (1+x)(1+x^2) = c /(1+x)+(dx+e)/(1+x^2)
tu as du degré 4 en haut, 3 en bas, on peut déjà sortir un polynôme de degré 1 de la fraction
f(x)= x^4 / (1+x)(1+x^2)
f(x)= ax+b +c /(1+x)+(dx+e)/(1+x^2)
a=1 en comparant les termes de degré le plus haut
x^4 / (1+x)(1+x^2) = x(x^3+x²+x+1) / (1+x)(1+x^2) - x(x²+x+1) / (1+x)(1+x^2)
= x - x(x²+x+1) / (1+x)(1+x^2)
= x - ( x(x²+x+1)+1-1) / (1+x)(1+x^2)
= x-1+1/ (1+x)(1+x^2)
il reste à décomposer 1/ (1+x)(1+x^2) = c /(1+x)+(dx+e)/(1+x^2)
Re: calcul de primitives
Bonjour,
(x+1)}=\dfrac{(x^2+1)(x+1)(x-1)}{(x^2+1)(x+1)}-\dfrac{1}{(x^2+1)(x+1)})
(x+1)}=x-1-\dfrac{1}{(x^2+1)(x+1)})
(x+1)}=\dfrac{Ax+B}{x^2+1}+\dfrac{C}{x+1})
ensuite pour déterminer les coefficients, tout dépend de ce que tu connais comme méthode
tu pourrais, par exemple, écrire :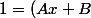(x+1)+C(x^2+1)) et procéder par identification mais il
et procéder par identification mais il
existe d'autres méthodes
ensuite pour déterminer les coefficients, tout dépend de ce que tu connais comme méthode
tu pourrais, par exemple, écrire :
existe d'autres méthodes
Re: calcul de primitives
NB :
si on a une forme P/Q, avec °P > °Q, il n'y a pas de dérivée classique qui a cette forme.
mais P/Q, avec °P ≤ °Q, on a du ln, de l’arc-tangente ...
d'où la transformation proposée obligatoire (sauf question préliminaire qui remplace cette recherche
si on a une forme P/Q, avec °P > °Q, il n'y a pas de dérivée classique qui a cette forme.
mais P/Q, avec °P ≤ °Q, on a du ln, de l’arc-tangente ...
d'où la transformation proposée obligatoire (sauf question préliminaire qui remplace cette recherche
Re: calcul de primitives
merci beaucoup pour vos réponses, si vous me permettez, je voudrais savoir comment on sait que la décomposition de 1/(1+x)(1+x^2) est de la forme (Ax+b)/(1+x^2)+C/(1+x) et non
C/(1+x^2)+(Ax+b)/(1+x) par exemple!
C/(1+x^2)+(Ax+b)/(1+x) par exemple!
Re: calcul de primitives
vois ici, par exemple, (c'est assez détaillé)
http://public.iutenligne.net/mathematiques/algebre/millaud/FractionsRationnelles.pdf
http://public.iutenligne.net/mathematiques/algebre/millaud/FractionsRationnelles.pdf
Re: calcul de primitives
on a par exemple dans C:
(x+1)}=\dfrac{A}{x+1}+\dfrac{B}{x-i}+\dfrac{C}{x+i})
comme le résultat est réel et la décomposition unique, en conjuguant, on a:
A réel,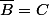
comme le résultat est réel et la décomposition unique, en conjuguant, on a:
A réel,
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
