Dérivée successive
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Anaisdeistres
- Membre Relatif
- Messages: 175
- Enregistré le: 29 Oct 2018, 19:37
-
 par Anaisdeistres » 07 Fév 2019, 16:47
par Anaisdeistres » 07 Fév 2019, 16:47
Bonjour,
Je cherche la dérivée successive de
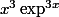
Merci.
-
aviateur
 par aviateur » 07 Fév 2019, 17:32
par aviateur » 07 Fév 2019, 17:32
Bonjour
On pose
=x^3e^{3x})
alors
}(x)=<br />3^n ( \frac{2 n}{27}-\frac{n^2}{9}+\frac{n^3}{27}-\frac{n x}{3}+\frac{n^2 x}{3}+n x^2+x^3)e^{3 x})
Pour le démontrer faire une récurrence.
-
Anaisdeistres
- Membre Relatif
- Messages: 175
- Enregistré le: 29 Oct 2018, 19:37
-
 par Anaisdeistres » 09 Fév 2019, 20:36
par Anaisdeistres » 09 Fév 2019, 20:36
Non je capte pas j'ai fait la formule de Leibniz mais je trouve pas pareil
-
aviateur
 par aviateur » 09 Fév 2019, 21:01
par aviateur » 09 Fév 2019, 21:01
Bonjour
Si tu connais la formule de Leibniz, je ne vois pas pourquoi tu ne capte pas.
Alors c'est à toi de mettre tes calculs.
-
rcompany
- Membre Naturel
- Messages: 70
- Enregistré le: 28 Oct 2018, 16:59
-
 par rcompany » 10 Fév 2019, 01:09
par rcompany » 10 Fév 2019, 01:09
On pose
}(x)=e^{3x}(a_nx^3+b_nx^2+c_nx+d_n),\text{ avec }(a_n), (b_n), (c_n)\;et\ (d_n))
des suites réelles
On montre facilement par récurrence qu'il existe
, (b_n), (c_n)\;et\ (d_n))
telles que pour tout n de

on a
}(x)=e^{3x}(a_nx^3+b_nx^2+c_nx+d_n))
Ensuite,
}(x)=e^{3x}\cdot (3a_{n-1}x^3+(3a_n+3b_n)x^2+(3c_n+2b_n)x+(3d_n+c_n)))
Et il reste donc à résoudre:
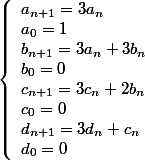
-
rcompany
- Membre Naturel
- Messages: 70
- Enregistré le: 28 Oct 2018, 16:59
-
 par rcompany » 11 Fév 2019, 13:35
par rcompany » 11 Fév 2019, 13:35
et
}(x)=3^{n-2}e^{3x}\cdot\big (9x^3+9nx^2+n(n-1)x+\frac{n^3-3n^2+2n}{3}\big))
-
Anaisdeistres
- Membre Relatif
- Messages: 175
- Enregistré le: 29 Oct 2018, 19:37
-
 par Anaisdeistres » 24 Fév 2019, 18:43
par Anaisdeistres » 24 Fév 2019, 18:43
Super merci beaucoup !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités