Vecteurs dm urgenttt

[Marion2167]

3 Exercice n 1 (7 points) :
On considere les points A(0;3), B(−1;1) et C(−4;2).
1. Determiner les coordonnées de I milieu de [BC].
2. Determiner les coordonnées du point D tel que 3−−→ DA +−−→ DB +−−→ DC = ~ 0. 3.
Demontrer que les points A, D et I sont alignes.
4. Calculer les coordonnées du point E appartenant `a l’axe des abscisses tel que les droites (BC) et (AE) soient paralleles.
Exercice n 1 (8 points) :
Placer sur une feuille quadrillee trois points A,B et C non alignes.
1. Placer le point P tel que −→ AP = −−−→ AB + 2−→ AC 2. Placer le point Q tel que −→ AQ = 3 2−−→ AB−3−→ AC
3. Que peut-on conjecturer pour les points A,P et Q?
4. (a) A quelle condition les points A, P et Q sont-ils alignes?
(b) Démontrer cette conjecture. Indication : une des methodes, une parmi d’autres, consiste a se placer dans les repere (A;B;C) et commencer par determiner les coordonnees des differents points.
Exercice n 3 (5 points)
On considere la fonction f qui a tout x reel associe 3x + 1 si x ≥ 0 sinon elle lui associe −3x + 1.
1. Calculer f(2),f(5),f(1 3) et f(−1 2).
2. Avec quel processus doit-on calculer f(0)?
3. Ecrire un algorithme permettant de calculer l’image de tout reel par cette fonction

[Lovahange12]

Salut,
Pour l'exercice 1:
1. La formule a utiliser est:
((xC-xB)/2;(yC-yB)/2)
2. Il faut que tu remplace les coordonnées de chaque point et tu trouve une équation.
Après j'ai besoin de savoir en quelle classe que tu es pour pas t'expliquer quelque chose qui n'est pas de ton niveau?

Exercice 3:
1. tu as juste à calculer f(2), f(5) et f(13) avec la formule 3x+1 et f(-12) avec -3x+1
2. Tu peut dire que on peut utiliser les 2 formule parce que quand on a x=0 les 2 formule nous donne le même résultat.
3. Pour moi l'algorithme ressemblerai à ça:
Entrée: x est un réel
Initialisation: a=3 , b=1 et c=-1
Traitement: Tant que x<=0 , alors:
affecter à x la valeur ax+b
Sinon:
affecter à x la valeur cx+b
Sortie:
afficher le résultat

[aymanemaysae]

Bonjour;

Exercice n° 1.

1.

Les coordonnées du point I sont : (- 1 - 4)/2 = - 5/2 = - 2,5 et (1 + 2)/2 = 3/2 = 1,5 .

2.

Soit D(x ; y) ;

donc :

donc :

donc : x = - 1 et y = 12/5 = 2,4 .

3.

On a :

et

donc et 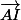sont colinéaires , donc les droites (AD) et (AI) sont parallèles .

Comme ces deux droites ont un point en commun qui est le point A , alors elles sont confondues ,

donc les points A , D et I se trouvent sur la même droite , donc ils sont alignés .

4.

Le coefficient directeur de la droite (BC) est : (2 - 1)/(- 4 - (- 1)) = - 1/3 .

Soit E(x ; 0) le point en question , donc le coefficient directeur de la droite (AE) est : (3 - 0)/(0 - x) = - 3/x .

Les deux droites (BC) et (AE) sont parallèles si leurs coefficients directeurs sont égaux ; donc on doit

avoir : - 3/x = - 1/3 ; donc : x = 9 .

[mathelot]

3 Exercice n 1 (7 points) :

1. Determiner les coordonnées de I milieu de [BC].

Salut,
Pour l'exercice 1:
1. La formule a utiliser est:
((xC-xB)/2;(yC-yB)/2)

c'est faux