Suite implicite

[leeri]

Bonjour, je me suis intéressée à un exercice dont la deuxième question me pose problème. Voici l’enoncé:
On considère l’équation d’inconnue X:
(1) X^5-X^3=n
1. Montrer que pour tout entier naturel non nul n, il existe un unique réel strictement positif xn vérifiant (1)
J’ai donc posé une fonction f(X)=X^5-X^3 et ai utilisé le théorème de la bijection.
2. Montrer qu’il existe des constantes a et b telles que xn=an^(1/5)+bn(-1/5)+o(n^(-1/5))
J’imagine qu’il faut exploiter la question précédente mais je ne vois pas comment.
Merci d’avance à ceux qui voudront bien m’aider à avancer

[aviateur]

Bonjour
On a

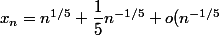Pour le démontrer c'est simple.

On pose

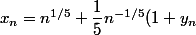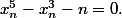
Puis on remplace: donc On développe et grâce à l'équation obtenue on montre que tend vers 0.

[guillaume100]

Salut,
Je mets xn=Xn comme ça c’est plus clair
Si tu mets X=Xn dans l’equation et que tu factorises à gauche par xn^5, alors en divisant par 1-Xn^(-2) (obtenu avec la factorisation), tu obtiens dans le membre de droite : n/(1-Xn^(-2))

Or Xn tend vers + l’infini (car n tend vers l’infini et x—> x^5 - x^3 est strictement croissante pour x assez grand), donc Xn^(-2) tend vers .....

Essaie alors de faire un développement limité de n/(1-Xn(-2)) et avec ça tu vas obtenir le premier membre de ton DL de Xn qui est égal à 1

Pour le deuxième, il suffit de placer ta nouvelle expression à la place de Xn et de réitérer le raisonnement

Normalement tu trouves a=1

[leeri]

Effectivement j’ai bien a=1 et b=1/5, merci!