Svp j'ai besoin d'aide c'est pour demain:
On considère la foncton: f(x)=3x/(x-2)
Df=]-∞,2[U]2,+∞[
On va montrer en utilisant la définition que lim f(x)=0 de x tend vers 0
càd Montrer que (∀ε>0) ((il existe)α>0) (∀x∈Df): 0<lxl<α⇒lf(x)l <ε
Limite
5 messages
- Page 1 sur 1
Re: Limite
Bonjour
Pour rester dans on a prendre
on a prendre 
Maintenant pour on a :
on a :
|= 3|x| \times \dfrac{1}{|x-2|}< 3|x| \times 1 = 3|x|.)
On voit que si de plus on a
on a |<\epsilon.)
En conclusion On obtient ce que l'on veut démontrer pour)
Pour rester dans
Maintenant pour
On voit que si de plus
En conclusion On obtient ce que l'on veut démontrer pour
Modifié en dernier par aviateur le 03 Fév 2019, 14:07, modifié 1 fois.
Re: Limite
Merci beaucoup, mais est ce que vous pouvez m'expliquer un peu en détaille si vous voulez
Re: Limite
La seule difficulté, peut être, c'est la majoration de 1/|x-2|
Si alors
alors 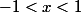 et
et  donc
donc 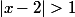 et
et 
Si
Modifié en dernier par aviateur le 03 Fév 2019, 14:05, modifié 1 fois.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
