Dénombrement - Triangle ternaire
19 messages
- Page 1 sur 1
Dénombrement - Triangle ternaire
Bonjour
Ce qui suit n'est pas vraiment une question, car j'ai enfin trouvé la réponse après beaucoup de réflexion. C'est plutôt une colle, assez difficile, que je propose à ceux qui sont intéressés. Pour la formuler clairement, je rappelle que "une n-liste d'éléments d'un ensemble E " est par définition, un élément du produit cartésien E xE.
Par exemple si E = {1, 2, 3, 4}, voici quelques 5-listes d'éléments de E :
(1, 1, 1, 1, 1)
(2, 1, 1, 2, 2)
(3, 4, 2, 2, 1)
1) Soit n et p deux entiers naturels tels que p <= n. Combien y a-t-il de n-listes de l'ensemble {0, 1} dont la somme des éléments vaut p ?
2) Soit n et p deux entiers naturels tels que p <= 2n. Combien y a-t-il de n-listes de l'ensemble {0, 1, 2} dont la somme des éléments vaut p ?
La difficulté est surtout dans la seconde question, la première question est une approche du sujet.
Bon courage
Pierre
Ce qui suit n'est pas vraiment une question, car j'ai enfin trouvé la réponse après beaucoup de réflexion. C'est plutôt une colle, assez difficile, que je propose à ceux qui sont intéressés. Pour la formuler clairement, je rappelle que "une n-liste d'éléments d'un ensemble E " est par définition, un élément du produit cartésien E xE.
Par exemple si E = {1, 2, 3, 4}, voici quelques 5-listes d'éléments de E :
(1, 1, 1, 1, 1)
(2, 1, 1, 2, 2)
(3, 4, 2, 2, 1)
1) Soit n et p deux entiers naturels tels que p <= n. Combien y a-t-il de n-listes de l'ensemble {0, 1} dont la somme des éléments vaut p ?
2) Soit n et p deux entiers naturels tels que p <= 2n. Combien y a-t-il de n-listes de l'ensemble {0, 1, 2} dont la somme des éléments vaut p ?
La difficulté est surtout dans la seconde question, la première question est une approche du sujet.
Bon courage
Pierre
Re: Dénombrement - Triangle ternaire
Salut,
Pour la première question je dirais:
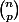
ensuite pour la deuxième, si p est pair:
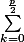
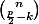
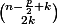
enfin si p est impair:
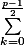
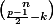
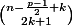
Pour la première question je dirais:
ensuite pour la deuxième, si p est pair:
enfin si p est impair:
Re: Dénombrement - Triangle ternaire
Je crois que ta formule ne fonctionne que si p < n . Mais elle donne effectivement le bon résultat dans ce cas (je l'ai testée sur une valeur numérique). Pourrais-tu nous dire en 2 mots comment tu as procédé ? Sans rentrer forcément dans des détails trop calculatoires.
PS
J'ai une formule plus simple, qui fonctionne pour p compris entre 0 et 2n.
PS
J'ai une formule plus simple, qui fonctionne pour p compris entre 0 et 2n.
Re: Dénombrement - Triangle ternaire
Bonjour
Je trouve
}^{E(p/2)} C_n^k C_{n-k}^{p-2 k})
ou encore
}^{E(p/2)}\dfrac{n!}{k! (k+n-p)! (-2 k+p)!})
Je trouve
ou encore
Modifié en dernier par aviateur le 31 Jan 2019, 18:47, modifié 1 fois.
Re: Dénombrement - Triangle ternaire
Bonjour.
J'ai testé cette formule avec n = 7 et p = 9 (nombre de 7-listes dont la somme des éléments vaut 9) et j'ai trouvé 581. La bonne réponse est 266. Donc je me suis trompé ou alors ... la formule n'est pas bonne ?
C'était un test avec la seconde formule. J'ai testé la première et là c'est bon ! Je me suis peut-être trompé avec l seconde ... Comment es-tu arrivé à ce résultat si ce n'est pas indiscret ?
J'ai testé cette formule avec n = 7 et p = 9 (nombre de 7-listes dont la somme des éléments vaut 9) et j'ai trouvé 581. La bonne réponse est 266. Donc je me suis trompé ou alors ... la formule n'est pas bonne ?
C'était un test avec la seconde formule. J'ai testé la première et là c'est bon ! Je me suis peut-être trompé avec l seconde ... Comment es-tu arrivé à ce résultat si ce n'est pas indiscret ?
Modifié en dernier par VieuxCrouton le 31 Jan 2019, 18:48, modifié 1 fois.
Re: Dénombrement - Triangle ternaire
Si ma formule donne 266 (la première) , la deuxième il y a un factoriel mal placé que j'ai remis à la bonne place.
Re: Dénombrement - Triangle ternaire
Voici une solution https://pierre18.freeboxos.fr:48784/share/l-r2hmkFCqLFByWV/Triangle.pdf
Pierre
Pierre
Modifié en dernier par VieuxCrouton le 02 Fév 2019, 17:20, modifié 6 fois.
Re: Dénombrement - Triangle ternaire
Il faut éviter de dire "la" solution. Comme si dans un problème il n'y avait qu'une solution et que celle que je donne et qui s'obtient en moins d'une minute n'en serait pas une.
Maintenant, regardes bien ma formule est bonne (tu peux vérifier avec quelques valeurs du tableau qui est ds le pdf)
Par contre leur formule finale est fausse. Tu peux vérifier!!!.
Maintenant, regardes bien ma formule est bonne (tu peux vérifier avec quelques valeurs du tableau qui est ds le pdf)
Par contre leur formule finale est fausse. Tu peux vérifier!!!.
Re: Dénombrement - Triangle ternaire
Excuse-moi de t'avoir froissé, je pensais faire plaisir à tout le monde en présentant ce problème et en me donnant le mal de poster ma solution. Je crois que je ne renouvellerai pas l'expérience.
Par ailleurs j'ai répondu à ton message et t'ai dit que ta formule est bonne (la première mais pas la seconde). Pourquoi te fâches tu ?
Et de qui parles-tu en disant "leur" formule ? Je ne vois qu'un seul autre intervenant et je lui ai bien dit que sa formule est bancale car elle ne fonctionne que si p < n. Mais elle n'est pas totalement fausse, il faut sûrement qu'il la revoie un peu.
Enfin je te fais remarquer que tu ne m'as pas donné ta solution, pas plus que l'autre intervenant d'ailleurs, bien que je vous l'ai demandé.
Par ailleurs j'ai répondu à ton message et t'ai dit que ta formule est bonne (la première mais pas la seconde). Pourquoi te fâches tu ?
Et de qui parles-tu en disant "leur" formule ? Je ne vois qu'un seul autre intervenant et je lui ai bien dit que sa formule est bancale car elle ne fonctionne que si p < n. Mais elle n'est pas totalement fausse, il faut sûrement qu'il la revoie un peu.
Enfin je te fais remarquer que tu ne m'as pas donné ta solution, pas plus que l'autre intervenant d'ailleurs, bien que je vous l'ai demandé.
Re: Dénombrement - Triangle ternaire
Je ne suis pas froissé du tout et il n'y a aucune raison de ne pas poser ce genre de problèmes, au contraire .
Mais je mets les points sur les i.
La solution de ton problème c'est presque immédiat et la formule que j'ai donnée est bonne, ensuite en recopiant la fraction avec les factorielles c'est la même sauf une erreur de copie.
Quant à la formule que je dis être fausse c'est celle du pdf.
(j'ai bien compris que FBLP avait donné une formule correcte pour p<n et en fait il a fait comme moi, j'ai simplement corrigé cela pour tenir du cas p>n).
Donc quand tu dis voici la solution, c'est normal que je dise qu'elle est fausse. C'est tout.
Mais je mets les points sur les i.
La solution de ton problème c'est presque immédiat et la formule que j'ai donnée est bonne, ensuite en recopiant la fraction avec les factorielles c'est la même sauf une erreur de copie.
Quant à la formule que je dis être fausse c'est celle du pdf.
(j'ai bien compris que FBLP avait donné une formule correcte pour p<n et en fait il a fait comme moi, j'ai simplement corrigé cela pour tenir du cas p>n).
Donc quand tu dis voici la solution, c'est normal que je dise qu'elle est fausse. C'est tout.
Re: Dénombrement - Triangle ternaire
Pourquoi dis-tu que ma formule est fausse ? Je l'ai testée et elle fonctionne bien. Pourrais-tu donner un peu plus de précision ?
Re: Dénombrement - Triangle ternaire
Ben non elle était pas bonne pour p impair. Je viens de la corriger. Pourrais-tu m'expliquer dans les grandes lignes comment tu es arrivé à ton résultat ?
Re: Dénombrement - Triangle ternaire
C'est tout simple : Cela vient de la formule)
Mais il faut que que k+(p-k)<=n soit positifs.
Donc les valeurs possibles de k vont max(0,n-p) à E(p/2).
Pour k donné il y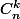 façon de placer le nombre 2 (dans le n-uplet) et il reste (p-2k) nbre 1 à placer dans les n-k places restantes du n_uplet i.e
façon de placer le nombre 2 (dans le n-uplet) et il reste (p-2k) nbre 1 à placer dans les n-k places restantes du n_uplet i.e 
d'où la formule.
Certes c'est direct mais l'utilisation de polynômes à son intérêt aussi.
Mais il faut que que k+(p-k)<=n soit positifs.
Donc les valeurs possibles de k vont max(0,n-p) à E(p/2).
Pour k donné il y
d'où la formule.
Certes c'est direct mais l'utilisation de polynômes à son intérêt aussi.
Re: Dénombrement - Triangle ternaire
Merci beaucoup pour cette démonstration, elle est très intéressante.
Je l'ai rajoutée en annexe au pdf. Dis-moi s'il y a une erreur.
Je l'ai rajoutée en annexe au pdf. Dis-moi s'il y a une erreur.
Re: Dénombrement - Triangle ternaire
Oui c'est ça.
Une petite remarque: quand tu dis p/2 "représente la division euclidienne de p par 2." Du point de vue littéraire c'est pas correct (même si on comprend ce que cela veut dire) .
Il faut dire "p/2" représente le quotient euclidien de p par 2". D'autre part ce n'est pas une notation usuelle.
La notation c'est E(p/2) , qui par ailleurs est la partie entière ("floor") de p/2.
Une petite remarque: quand tu dis p/2 "représente la division euclidienne de p par 2." Du point de vue littéraire c'est pas correct (même si on comprend ce que cela veut dire) .
Il faut dire "p/2" représente le quotient euclidien de p par 2". D'autre part ce n'est pas une notation usuelle.
La notation c'est E(p/2) , qui par ailleurs est la partie entière ("floor") de p/2.
 Re: Dénombrement - Triangle ternaire
Re: Dénombrement - Triangle ternaire
Salut,
En fait, "la" généralisation usuelle des coefficients binomiaux, c'est la notion de coefficients multinomiaux (<- lien) qui correspond au nombre de façon de partitionner un ensemble à éléments en parties contenant respectivement
éléments en parties contenant respectivement  éléments (avec
éléments (avec  ) et qui, bien sûr, correspondent aussi aux coefficients que l'on obtient lorsque l'on développe
) et qui, bien sûr, correspondent aussi aux coefficients que l'on obtient lorsque l'on développe ^k) .
.
Et si on connaît cette notion de coefficient multinomial, la réponse à ton truc est immédiate vu qu'il suffit de considérer tout les triplets d'entiers naturels) tels que
tels que  et
et  et de sommer les coefficients multinomiaux
et de sommer les coefficients multinomiaux  correspondant pour avoir le nombre de façon de répartir les 0 ; 1 et 2 sur les
correspondant pour avoir le nombre de façon de répartir les 0 ; 1 et 2 sur les  places.
places.
Et bien sûr, c'est exactement la même chose avec un ensemble de départ quelconque. Par exemple, le nombre de listes de {1,3,4,7} dont la somme fait
listes de {1,3,4,7} dont la somme fait  , c'est la somme des
, c'est la somme des  prise sur l'ensemble des quadruplets d'entiers naturels
prise sur l'ensemble des quadruplets d'entiers naturels ) tels que
tels que  et
et 
Ensuite, si on veut, on peut paramétrer l'ensemble des) (mais c'est pas forcément malin en ce qui concerna la compréhension de la formule) en écrivant par exemple que
(mais c'est pas forcément malin en ce qui concerna la compréhension de la formule) en écrivant par exemple que 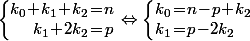 avec
avec \!\leq\!k_2\!\leq\!\frac{p}{2}) pour que
pour que  soient
soient 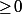 .
.
En fait, "la" généralisation usuelle des coefficients binomiaux, c'est la notion de coefficients multinomiaux (<- lien) qui correspond au nombre de façon de partitionner un ensemble à
Et si on connaît cette notion de coefficient multinomial, la réponse à ton truc est immédiate vu qu'il suffit de considérer tout les triplets d'entiers naturels
Et bien sûr, c'est exactement la même chose avec un ensemble de départ quelconque. Par exemple, le nombre de
Ensuite, si on veut, on peut paramétrer l'ensemble des
Modifié en dernier par Ben314 le 01 Fév 2019, 21:00, modifié 2 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Dénombrement - Triangle ternaire
aviateur a écrit:... D'autre part ce n'est pas une notation usuelle.
La notation c'est E(p/2) , qui par ailleurs est la partie entière ("floor") de p/2.
J'ai corrigé, merci
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
