Pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
22 messages
- Page 1 sur 2 - 1, 2
 pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
n est naturel positif, il faut trouver tous les n tels que n⁴+n³+n²+n+1 est un carré parfait.
3 est une solution. Y-en a-t-il d'autres ?
Factoriser le polynome donne des nombres rationnels, donc ça n'aide pas. Sinon j'ai essayé de l'encadrer avec d'autres carrés, mais ça ne fonctionne pas non plus. Si on écrit n⁴+n³+n²+n+1 =a², on a (n²+n)(n²+1)=(a+1)(a-1), mais je ne vois pas comment résoudre le problème. Merci de m'aider !
3 est une solution. Y-en a-t-il d'autres ?
Factoriser le polynome donne des nombres rationnels, donc ça n'aide pas. Sinon j'ai essayé de l'encadrer avec d'autres carrés, mais ça ne fonctionne pas non plus. Si on écrit n⁴+n³+n²+n+1 =a², on a (n²+n)(n²+1)=(a+1)(a-1), mais je ne vois pas comment résoudre le problème. Merci de m'aider !
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
Bonjour si on a n⁴+n³+n²+n+1 =a², posons b=8a (a entier) alors
64(n⁴+n³+n²+n+1)=^2 =(8 n^2+4n +3)^2+40 n+55)
i. e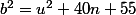 ou
ou 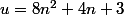
On ne peut pas avoir 40 n+55=0 donc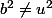 et alors
et alors 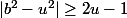
i.e
Une petite étude montre que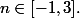 c.q.f.d
c.q.f.d
64(n⁴+n³+n²+n+1)=
i. e
On ne peut pas avoir 40 n+55=0 donc
i.e
Une petite étude montre que
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
Coucou,
Comment trouves-tu l'inégalité |b²-u²|>2u-1 ?
Comment trouves-tu l'inégalité |b²-u²|>2u-1 ?
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
Salut,
^2\!=\!u^2\!+\!2u\!+\!1) .
.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
Bonjour, oui 'est ça.
En fait je ne me suis pas fatigué. Les carrés les plus proches de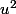 sont
sont ^2) et
et ^2.)
La différence dans les cas sont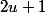 et
et 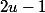 . Donc en général, la distance de tout carré distinct de
. Donc en général, la distance de tout carré distinct de 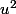 et supérieure où égale à |2u-1| (= 2u-1 ici car u>1).
et supérieure où égale à |2u-1| (= 2u-1 ici car u>1).
En fait je ne me suis pas fatigué. Les carrés les plus proches de
La différence dans les cas sont
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
Et dans le cas où la somme de puissance de  s'arrête à un nombre impair, par exemple
s'arrête à un nombre impair, par exemple 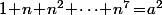 ou bien
ou bien 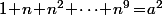 , vous faîtes comment ?
, vous faîtes comment ?
(éventuellement à déplacer dans les "énigmes" : je pense savoir faire ces deux cas là, mais je sais pas si je saurais traiter le cas général . . .)
(éventuellement à déplacer dans les "énigmes" : je pense savoir faire ces deux cas là, mais je sais pas si je saurais traiter le cas général . . .)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
Bonjour
La démarche pour n pair ne va plus. On fait donc différemment en utilisant l'expression factorisée. Par exemple pour n=7
on a(n^2 +1)(n^4+1)=a^2.)
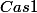 n est pair. Un diviseur premier p de a (donc différent de 2) a son carré qui divise l'un des 3 facteur. (Pour le voir, il suffit de supposer que ce n'est pas le cas et arriver à une contradiction ).
n est pair. Un diviseur premier p de a (donc différent de 2) a son carré qui divise l'un des 3 facteur. (Pour le voir, il suffit de supposer que ce n'est pas le cas et arriver à une contradiction ).
On en déduit que chaque facteur est un carré parfait. C'est assez facile de voir que n^2+1 ne peut être un carré parfait.
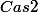 n est impair. Mais alors l'exposant de 2 dans
n est impair. Mais alors l'exposant de 2 dans(n^2 +1)(n^4+1)) est impair. imp.
est impair. imp.
On doit pourvoir généraliser
La démarche pour n pair ne va plus. On fait donc différemment en utilisant l'expression factorisée. Par exemple pour n=7
on a
On en déduit que chaque facteur est un carré parfait. C'est assez facile de voir que n^2+1 ne peut être un carré parfait.
On doit pourvoir généraliser
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
J'ai un peu des doutes là :aviateur a écrit:n est impair. Mais alors l'exposant de 2 dans
est impair.
Comme
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?


Le raisonnement du cas 1 reste valable pour p diviseur de a
Cela conduit à
On pose alors
se simplifie pour donner
La résolution de cette équation donne :
On est amené à résoudre ce problème annexe voir pour quels m
Là je n'ai pas le temps de finir mais le polynôme en m est pair. On peut surement chercher les solutions en suivant le même procédé que j'ai fait pour pour la question initiale.
Alors je pense qu'on trouver un nombre fini de solution (nombre assez petit) et normalement pouvoir finir la question.
Remarque: @ben aurais-tu résolu cela autrement?
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
Non, j'ai fait plus ou moins pareil, sauf que dans le cas impair, j'ai vérifié que les trois entiers n+1 ; (n^2+1)/2 et (n^4+1)/2 étaient 2 à 2 premiers entre eux et comme leur produit est le carré (2a)^2 c'est qu'en fait c'est tout les 3 des carrés et ça te fait un max d'équations "peu compatibles" dont certaines un peu plus simple que la tienne.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
aviateur a écrit:Bonjour si on a n⁴+n³+n²+n+1 =a², posons b=8a (a entier) alors
64(n⁴+n³+n²+n+1)=
i. eou
On ne peut pas avoir 40 n+55=0 doncet alors
i.e
Une petite étude montre quec.q.f.d
Salut,
Une petite explication pour l'intuition derrière le fait de poser b=8a ?
C'est un peu miraculeux sur la suite :p
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
salut
J'étais arrivé à ce 64 en écrivant
^2+(cn+d))
on trouve a=1/2, b=3/8, c=5/8 et d=55/64
d'où l'intérêt de multiplier les deux membres par 64
Mais je n'étais pas allé plus loin.
J'étais arrivé à ce 64 en écrivant
on trouve a=1/2, b=3/8, c=5/8 et d=55/64
d'où l'intérêt de multiplier les deux membres par 64
Mais je n'étais pas allé plus loin.
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
Oui @chen a expliqué pourquoi. Il n'y a rien de miraculeux: on multiplie par 64 pour continuer à travailler avec les entiers.
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
chan79 a écrit:salut
J'étais arrivé à ce 64 en écrivant
on trouve a=1/2, b=3/8, c=5/8 et d=55/64
d'où l'intérêt de multiplier les deux membres par 64
Mais je n'étais pas allé plus loin.
Merci c'est simple !
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
Salut.
Plus ou moins le même type d'idée: en posant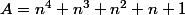 , on a
, on a
^2=n^4+n^3+\frac{1}{4}n^2<A)
et
^2=n^4+n^3+\frac{9}{4}n^2+n+1>A) (sauf pour n=0)
(sauf pour n=0)
donc, si est pair,
est pair, 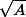 est strictement compris entre 2 entiers consécutifs donc n'est pas entier, et si
est strictement compris entre 2 entiers consécutifs donc n'est pas entier, et si  est impair, l'unique valeur entiere possible pour
est impair, l'unique valeur entiere possible pour 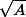 est l'entier
est l'entier 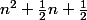 , et alors
, et alors
^2=n^4+n^3+\frac{5}{4}n^2+\frac{1}{2}n+\frac{1}{4}) , donc en simplifiant,
, donc en simplifiant, 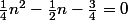 , ce qui donne
, ce qui donne 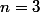 ou
ou 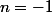 (exclu si on ne regarde que les entiers positifs)
(exclu si on ne regarde que les entiers positifs)
Plus ou moins le même type d'idée: en posant
et
donc, si
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
Peut on montrer que pour tout 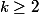 , l'équation
, l'équation 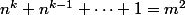 a un nombre fini de solutions?
a un nombre fini de solutions?
edit: la réponse est oui, et vous avez déjà fait une bonne partie du boulot
edit 2: bon en fait il me reste un cas à traiter...mais qu'il me semble Ben a déjà réussi si je décrypte bien ses messages
edit 3: je n'arrive par exemple pas encore à résoudre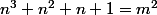
edit: la réponse est oui, et vous avez déjà fait une bonne partie du boulot
edit 2: bon en fait il me reste un cas à traiter...mais qu'il me semble Ben a déjà réussi si je décrypte bien ses messages
edit 3: je n'arrive par exemple pas encore à résoudre
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
ffback a écrit:Peut on montrer que pour tout, l'équation
a un nombre fini de solutions?
edit: la réponse est oui, et vous avez déjà fait une bonne partie du boulot
edit 2: bon en fait il me reste un cas à traiter...mais qu'il me semble Ben a déjà réussi si je décrypte bien ses messages
edit 3: je n'arrive par exemple pas encore à résoudre
Message assez comique, voire incompréhensible:
edi1 et edit2 admettons.
edit 3 après avoir dit edit1 et edit2, tu ne sait pas faire le cas le plus facile!!
Si tu combines, la solution que j'ai donnée pour k=7 et celui de ben, il n'y a pas de problème pour k=3.
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
Je pense que si j'arrive à faire ce "cas facile" alors j'arrive à faire tous les autres. (J'avais effectivement oublié ce cas, d'où mes edit)
Ta solution pour le cas k=7 à un gap. Il reste à voir quand les valeurs d un certain poly de degré pair est un carré et tu dis qu'on doit pouvoir probablement adapter la première méthode, mais cette méthode ne marche bien que si le coeff dominant est un carré, ce qui n'est plus le cas.
Quant à la méthode de Ben, bah je veux bien le croire mais elle manque un peu de détails...et je ne sais pas si elle marche pour k=3 (car on obtient moins d equations)
Ta solution pour le cas k=7 à un gap. Il reste à voir quand les valeurs d un certain poly de degré pair est un carré et tu dis qu'on doit pouvoir probablement adapter la première méthode, mais cette méthode ne marche bien que si le coeff dominant est un carré, ce qui n'est plus le cas.
Quant à la méthode de Ben, bah je veux bien le croire mais elle manque un peu de détails...et je ne sais pas si elle marche pour k=3 (car on obtient moins d equations)
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
Ben314 a écrit:J'ai un peu des doutes là :aviateur a écrit:n est impair. Mais alors l'exposant de 2 dans
est impair.
Commeet
sont impairs, on a
donc la valuation 2-adique de
est 2, mais par contre tout ce qu'on peut dire de celle de
c'est qu'elle est
mais elle peut évidement être paire ou impaire.
Coucou !
ça doit être un peu différent en effet.
J'ai l'impression qu'une stratégie générale pour aborder ce genre d'équations c'est d'élargir un peu l'anneau
Ici il faudrait donc se placer dans
Si on s'arrête à un nombre n tel que n+1 n'est pas premier (en particulier n impair) la somme de gauche n'est pas l'évaluation d'un polynôme cyclotomique en n et donc je pense qu'il faut se placer dans des anneaux de la forme
Je n'ai pas regardé en détail mais je regarderai si ça marche quand j'aurai deux minutes.
Re: pour quel n est n⁴+n³+n²+n+1 un carré parfait ?
Je vais expliquer pourquoi le cas 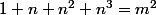 implique les autres.
implique les autres.
On considére=1+n+\cdots+n^k=\frac{n^{k+1}-1}{n-1}\)
Premier cas : pair.
pair.
C'est essentiellement la même démarche que celle déjà faite, qui marcherait en fait pour tout polynôme A de degré pair unitaire: on peut trouver 2 polynômes et
et  à coefficients rationnels avec
à coefficients rationnels avec  unitaire, tels que
unitaire, tels que =Q(x)^2+R(x)) et
et <deg(Q)) . Il suffit pour cela de définir de proche en proche les coefficients de Q, en commençant par le plus haut. Ensuite on multiplie tout par
. Il suffit pour cela de définir de proche en proche les coefficients de Q, en commençant par le plus haut. Ensuite on multiplie tout par 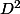 où
où  est le ppcm des dénominateurs de Q et R: ainsi
est le ppcm des dénominateurs de Q et R: ainsi 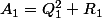 avec
avec =D^2A(x)) ,
, =DQ(x)) et
et =D^2R(x)) , de sorte que ces nouveaux polynômes sont à coefficients entiers. Ceci fait, on déduit du fait que
, de sorte que ces nouveaux polynômes sont à coefficients entiers. Ceci fait, on déduit du fait que ) est négligeable devant
est négligeable devant ) que pour
que pour  assez grand,
assez grand, -1)^2<A_1(n)<(Q_1(n)+1)^2) , et que donc
, et que donc ) (et donc
(et donc ) ) n'est pas un carré excepté si
) n'est pas un carré excepté si =Q_1(n)^2) et donc
et donc =R(n)=0) . Mais si ça arrive pour une inifinité de n c'est donc qu'en fait
. Mais si ça arrive pour une inifinité de n c'est donc qu'en fait =Q(x)^2) est un carré, ce qui n'est pas le cas ici (par ex car les racines de A sont simples)
est un carré, ce qui n'est pas le cas ici (par ex car les racines de A sont simples)
Il y a donc seulement un nombre fini d'entiers telles que
telles que ) soit un carré.
soit un carré.
On considére
Premier cas :
C'est essentiellement la même démarche que celle déjà faite, qui marcherait en fait pour tout polynôme A de degré pair unitaire: on peut trouver 2 polynômes
Il y a donc seulement un nombre fini d'entiers
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
