MERCI BEAUCOUP de m'aider a résoudre l'equation trigonométrique suivante :
tg(4x)+tg(x) = tg(3x)+tg(2x)
Une autre equation trigonométrique
6 messages
- Page 1 sur 1
Re: Une autre equation trigonométrique
Bonjour
Si tu poses f(x)=tan(4x)+tan(x)-(tan(3x)+tan(2x))
On voit que l'équation est f(x)=0.
Mais f est impaire donc si x est solution -x aussi. D'autre part f est périodique donc pour avoir toutes les solutions il suffit de résoudre sur
périodique donc pour avoir toutes les solutions il suffit de résoudre sur 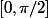
Or sur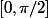 il y a exactement 2 solutions
il y a exactement 2 solutions 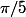 et
et 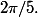
On en déduit que l'ensemble des solutions est :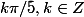
Si tu poses f(x)=tan(4x)+tan(x)-(tan(3x)+tan(2x))
On voit que l'équation est f(x)=0.
Mais f est impaire donc si x est solution -x aussi. D'autre part f est
Or sur
On en déduit que l'ensemble des solutions est :
Re: Une autre equation trigonométrique
Parce que quand le dénominateur n'est pas nul (et aussi tan(a) tan(b) ont un sens) on a tan(a+b)=(tan(a)+tan(b))/(1-tan(a) tan(b))
Donc tan(4x)+tan(x) s'exprime avec tan(5x) mais aussi tan(3x)+tan(2x).
Autrement dit on peut mettre tan(5x) en facteur ds f.
Donc tan(4x)+tan(x) s'exprime avec tan(5x) mais aussi tan(3x)+tan(2x).
Autrement dit on peut mettre tan(5x) en facteur ds f.
Re: Une autre equation trigonométrique
Une autre façon de faire pour éviter l'étude des variation de f , c'est d'exprimer touts les tangentes en fonction de la seule tan(x) avec la formule du message précédent.
En posant t=tan(x) ça m'étonnerait pas que l'équation est facile en t.
En posant t=tan(x) ça m'étonnerait pas que l'équation est facile en t.
Re: Une autre equation trigonométrique
Salut,
Perso, j'aurais écrit que\!+\!\tan(b)=\dfrac{\sin(a)}{\cos(a)}\!+\!\dfrac{\sin(b)}{\cos(b)}=\dfrac{\sin(a)\cos(b)\!+\!\cos(a)\sin(b)}{\cos(a)\cos(b)}=\dfrac{\sin(a\!+\!b)} {\cos(a)\cos(b)})
\cos(b)\!=\!\frac{1}{2}\big(\cos(a\!+\!b)\!+\!\cos(a\!-\!b)\big)\ \text{de fa\c con \`a avoir})
\!+\!\tan(x)\!=\!\tan(3x)\!+\!\tan(2x)\ \Leftrightarrow\ \dfrac{2\sin(5x)} {\cos(5x)\!+\!\cos(3x)}\!=\!\dfrac{2\sin(5x)} {\cos(5x)\!+\!\cos(x)}\cr\hskip10mm\Leftrightarrow\ \sin(5x)\!=\!0\ \text{ ou bien }\ \cos(3x)\!=\!\cos(x)\ \text{ (et les 4 d\'enominateur non nuls)})
- L'équation\!=\!0) a pour solutions les
a pour solutions les 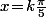 avec
avec 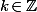 (et les dénominateur sont non nul).
(et les dénominateur sont non nul).
- L'équation\!=\!\cos(x)) a pour solutions les
a pour solutions les 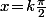 avec
avec 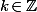 sauf que, si
sauf que, si  est impair, le dénominateur
est impair, le dénominateur ) est nul et que, si
est nul et que, si  est pair, c'est une solution déjà trouvée dans le premier cas.
est pair, c'est une solution déjà trouvée dans le premier cas.
Perso, j'aurais écrit que
- L'équation
- L'équation
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 105 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
